

| A. | -$\frac{1}{198}$ | B. | -$\frac{1}{200}$ | C. | $\frac{1}{200}$ | D. | $\frac{1}{202}$ |
分析 观察各行的规律,可得:分数符号的规律,即当分母是奇数时,为正号.当分母是偶数时,符号是负号.所有的分子都是1.分母是从1开始连续的整数,第n行末尾的分母即是1+2+3+…+n=$\frac{n(n+1)}{2}$.根据这一规律,计算第19行末尾数的分母是$\frac{19×20}{2}$=190,则第20行从左至右第10个数的分母是190+10=200,则该分数是-$\frac{1}{200}$.
解答 解:∵分子都是1,分母是从1开始连续的整数,第n行末尾的分母即是1+2+3+…+n=$\frac{n(n+1)}{2}$,
∴第19行末尾数的分母是$\frac{19×20}{2}$=190,
∴第20行从左至右第10个数的分母是190+10=200,则该分数是-$\frac{1}{200}$.
故选:B.
点评 此题考查数字的变化规律,找出数字之间的运算规律,利用规律解决问题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
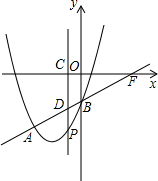 如图所示,抛物线y=x2+bx+c与直线y=x-1交于A、B两点,点A的纵坐标为-4,点B在y轴上,直线AB与x轴交于点F,点P是线段AB下方的抛物线上一动点,横坐标为m,过点P作PC⊥x轴于C,交直线AB于D.
如图所示,抛物线y=x2+bx+c与直线y=x-1交于A、B两点,点A的纵坐标为-4,点B在y轴上,直线AB与x轴交于点F,点P是线段AB下方的抛物线上一动点,横坐标为m,过点P作PC⊥x轴于C,交直线AB于D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲乙两人同时登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
甲乙两人同时登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能比较 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com