
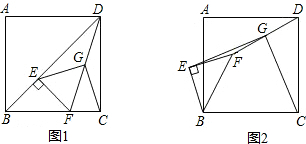
分析 (1)根据直角三角形斜边中线可迅速得出结论;
(2)连接AC、BD交于点M,过点E作EH⊥BF于点H,连接GH、GM,证明△EHG≌△GMC即可.
解答 解:(1)如图1,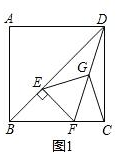
∵EF⊥BD,G为DF中点,
∴EG为Rt△EFD斜边中线,
∴EG=DG=GF,
∴∠GED=∠GDE,
同理GC=GD=GF,∠GDC=∠GCD,
∴EG=CG,
∵∠EGF=∠GDE+∠GED=2∠GDE,
∠FGC=∠GDC+∠GCD=2∠GDC,
∴∠EGC=2∠GDE+2∠GDC=2(∠GDE+∠GDC),
∵∠GDE+∠GDC=45°,
∴∠EGC=90°;
(2)成立.
如图2,连接AC、BD交于点M,过点E作EH⊥BF于点H,连接GH、GM,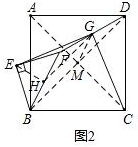
∵四边形ABCD是正方形,
∴AC=BD,AC⊥BD,AM=CM=BM=DM,
∵△BEF是等腰直角三角形,
∴EH=FH=BH,
∵G是DF的中点,
∴GH∥BD,GH=BM=DM=AM=CM,
GM∥BF,GM=BH=FH=EH,
∴∠FHG=∠FBM=∠GMD,
∵∠EHG=90°+∠FHG,
∠GMC=90°+∠GMD,
∴∠EHG=∠GMC,
在△EHG和△GMC中,
$\left\{\begin{array}{l}{HG=MC}\\{∠EHG=∠GMC}\\{EH=GM}\end{array}\right.$,
∴△EHG≌△GMC(SAS),
∴EG=CG,∠EGH=∠GCM,
∵GH∥BD,AC⊥BD,
∴AC⊥GH,
∴∠HGM+∠GMA=90°,
∵∠GMA=∠GCM+∠MGC,
∴∠HGM+∠GCM+∠MGC=90°,
∴∠EGH+∠HGM+∠MGC=90°,
即EG⊥CG.
点评 本题考查了正方形的性质、旋转的性质、等腰直角三角形的性质、中位线的性质、全等三角形的判定与性质等知识点,难度较大,尤其是第(2)问,不易想到.其实,本题体现了“中点”的经典用法,在初中阶段,与“中点”有关的知识点和方法并不多,同学们可自行总结一下.本题用到的与“中点”有关的知识点主要是:等腰三角形三线合一、直角三角形斜边中线定理、中位线定理.若同学们熟悉这些知识点,那么辅助线也容易想到,第(2)问也会变得简单.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:解答题
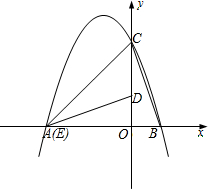 如图,二次函数y=ax2+bx+c的图象交x轴于A、B两点,交y轴于点C.且B(1,0),若将△BOC绕点O逆时针旋转90°,所得△DOE的顶点E恰好与点A重合,且△ACD的面积为3.
如图,二次函数y=ax2+bx+c的图象交x轴于A、B两点,交y轴于点C.且B(1,0),若将△BOC绕点O逆时针旋转90°,所得△DOE的顶点E恰好与点A重合,且△ACD的面积为3.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
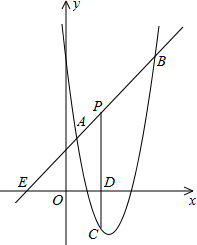 如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A($\frac{1}{2}$,$\frac{5}{2}$)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.当△PAC为直角三角形时点P的坐标(3,5)或($\frac{7}{2}$,$\frac{11}{2}$).
如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A($\frac{1}{2}$,$\frac{5}{2}$)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.当△PAC为直角三角形时点P的坐标(3,5)或($\frac{7}{2}$,$\frac{11}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | … | 0 | 1 | 2 | … |
| y | … | 4 | -4 | 6 | … |
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | -$\frac{1}{198}$ | B. | -$\frac{1}{200}$ | C. | $\frac{1}{200}$ | D. | $\frac{1}{202}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
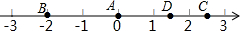 如图所示,A、B、C、D四点在数轴上分别表示有理数a、b、c、d,则大小顺序正确的是( )
如图所示,A、B、C、D四点在数轴上分别表示有理数a、b、c、d,则大小顺序正确的是( )| A. | a<b<c<d | B. | b<a<d<c | C. | a<b<d<c | D. | d<c<b<a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com