
【题目】在平面直角坐标系中,点![]() ,
,![]() .
.
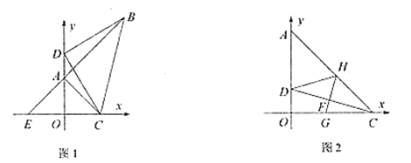
(1)若![]() ,
,![]() 满足
满足![]() .
.
①直接写出![]() ______,
______,![]() ______.
______.
②如图1,![]() 为点
为点![]() 上方一点,连接
上方一点,连接![]() ,在
,在![]() 轴右侧作等腰
轴右侧作等腰![]() ,
,![]() ,连接
,连接![]() 并延长交
并延长交![]() 轴于点
轴于点![]() ,当点
,当点![]() 上方运动时,求
上方运动时,求![]() 的面积;
的面积;
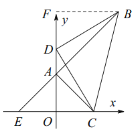
(2)如图2,若![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() ,
,![]() 为
为![]() 上一点,且
上一点,且![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .连接
.连接![]() ,当
,当![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)①![]() ;②16;(2)
;②16;(2)![]() .
.
【解析】
(1)①解方程组求出m,n即可.
②过点![]() 作
作![]() 轴于点
轴于点![]() ,设
,设![]() ,证明
,证明![]() ,可得BF=OD,FD=OC,用t表示OD,AF,BF,得出AF=BF,根据等腰三角形的判定得
,可得BF=OD,FD=OC,用t表示OD,AF,BF,得出AF=BF,根据等腰三角形的判定得![]() 是等腰直角三角形,再由平行线的性质得出
是等腰直角三角形,再由平行线的性质得出![]() 是等腰直角三角形,则EO=OC=AO=4,由此即可解决问题.
是等腰直角三角形,则EO=OC=AO=4,由此即可解决问题.
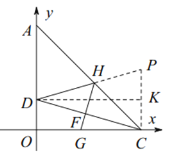
(2)如图2中,作CP∥OA交DH的延长线于P,作DK⊥CP于K.证明△HCG≌△HCP(AAS),推出CG=CP,由此构建方程即可解决问题.
解:(1)①![]() ,解得
,解得![]() ,
,
故答案为:![]() ;
;
②过点![]() 作
作![]() 轴于点
轴于点![]() ,设
,设![]() ,
,
∴∠BFD=∠DOC=90°,∠BDF+∠DBF=90°,
∵![]() ,
,
∴∠BDF+∠CDO=90°,
∴∠CDO=∠DBF,
∵等腰![]() ,
,
∴DB=CD,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 是等腰直角三角形,∠FBA=45°,
是等腰直角三角形,∠FBA=45°,
∵![]()
∴BF∥x轴,
∴∠OEA=∠FBA=45°,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴EO=OC=AO=4,,
∴![]() 的面积为:
的面积为:![]() =16;
=16;
(2)作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,
则![]() ,
,![]() ,
,
又![]() ,
,
∴![]() ,
,
∴![]() 是等腰三角形.
是等腰三角形.
作![]() 于点
于点![]() ,则
,则![]() ,
,
由平移可得![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
∵∠CGH+∠OCD=90°,∠ODC+∠OCD=90°,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴∠CGH=∠P,
∵![]() ,
,![]() ,
,
∴∠GCH=∠OAC =∠PCH,
又∵CH=CH
∴![]() ,
,
∴![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.


科目:初中数学 来源: 题型:
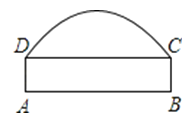
【题目】如图,四边形ABCD中,AB=BC=2CD,AB∥CD,∠C=90°,E是BC的中点,AE与BD相交于点F,连接DE
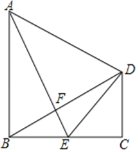
(1)求证:△ABE≌△BCD;(2)若CD=1,试求△AED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了深入贯彻党的十九大精神,我县某中学开展了十九大精神进校园知识气赛活动,特对本校部分学生(随机抽样)进行了一次相关知识的测试(成绩分为A,B,C,E五个组,x表示测试成绩),通过对测试成绩的分析得到如图所示的两幅不完整的统计图,请你根据图中提供的信息解答以下问题:
A组:90≤x≤100
B组:80≤x<90
C组:70≤x<80
D组:60≤x<70
E组:x<60
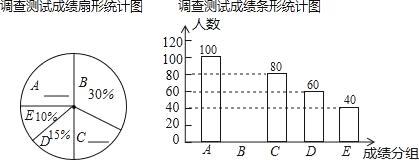
(1)参加调查测试的学生共有 人,扇形C的圆心角的度数是; .
(2)请将两幅统计图补充完整;
(3)本次调查测试成绩的中位数落在哪个小组内,说明理由;
(4)本次调查测试成绩在80分以上(含80分)为优秀,该中学共有3000人,请估计全校测试成绩为优秀的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分8分)
如图,用两段等长的铁丝恰好可以分别围成一个正五边形和一个正六边形,其中正五边形的边长为(![]() )
)![]() ,正六边形的边长为(
,正六边形的边长为(![]() )cm(其中
)cm(其中![]() ),求这两段铁丝的总长
),求这两段铁丝的总长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
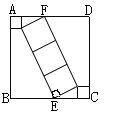
【题目】如图,在边长为7的正方形ABCD中放入五个小正方形后形成一个中心对称图形,其中两顶点E、F分别在边BC、AD上,则放入的五个小正方形的面积之和为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一条双向公路隧道,其横断面由抛物线和矩形ABCD的三边DA、AB、BC围成,隧道最大高度为4.9米,AB=10米,BC=2.4米,若有一辆高为4米、宽为2米的集装箱的汽车要通过隧道,为了使箱顶不碰到隧道顶部,又不违反交通规则(汽车应靠道路右侧行驶,不能超过道路中线),汽车的右侧必须离开隧道右壁几米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com