
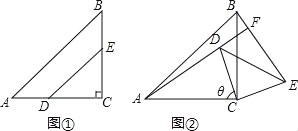
【题目】如图①,在△ABC中,∠ACB=90°,AC=BC,在AC、BC边上分别截取CD=CE,连结DE.将△DCE绕着点C顺时针旋转θ角,连结BE、AD.
(1)当0°<θ<90°时,如图②,直线BE交直线AD于点F.
①求证:△ACD≌△BCE.
②求证:AF⊥BE.
(2)当0°<θ<360°,AC=5,CD=3,四边形CDFE是正方形时,直接写出AF的长度.
【答案】(1)证明见解析;(2)1.
【解析】
试题分析: (1)①根据旋转的性质和已知,运用SAS证明即可;②由问题原型中的结论:△ACE≌△BCE得出∠BFO=∠ACB,结合等量代换进行求解即可;
(2)运用CD∥BE结合初步探究中的结论,可证CD⊥AF,结合勾股定理即可求解.
试题解析:(1)①如图②,
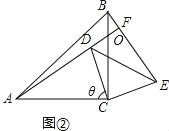
∵△DCE绕着点C顺时针旋转θ角,由旋转的性质可知,
∴∠ACD=∠BCE=θ,
又∵AC=BC,CD=CE,
在△ACD和△BCE中,
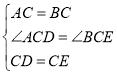 ,
,
∴△ACD≌△BCE;
②如图②,设AF与BC交点于O,
∵△ACD≌△BCE,
∴∠DAC=∠EBC,
∵∠AOC=∠BOF,
∴∠BFO=∠ACB=90°,
∴AF⊥BE;
(2)如图③,
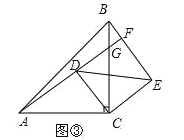
∵AC=5,CD=3,四边形CDFE是正方形时,
∵AD⊥CD,
∴AD=![]() ,
,
∴AF=4+3=7,
如图4,
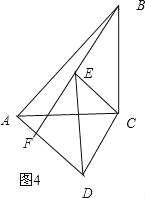
∴AF=4﹣3=1.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A. 过一点有且只有一条直线与已知直线垂直
B. 三角形任意两边之和小于第三边
C. 三角形的一个外角大于它的任何一个内角
D. 平行与同一条直线的两直线平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列一元二次方程中,没有实数根的是( )
A. 4x2﹣5x+2=0 B. x2﹣6x+9=0 C. 5x2﹣4x﹣1=0 D. 3x2﹣4x+1=0
查看答案和解析>>
科目:初中数学 来源: 题型:
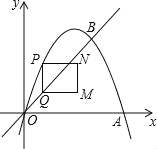
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx与x轴交于O、A两点,与直线y=x交于点B,点A、B的坐标分别为(3,0)、(2,2).点P在抛物线上,过点P作y轴的平行线交射线OB于点Q,以PQ为边向右作矩形PQMN,且PN=1,设点P的横坐标为m(m>0,且m≠2).
(1)求这条抛物线所对应的函数表达式.
(2)求矩形PQMN的周长C与m之间的函数关系式.
(3)当矩形PQMN是正方形时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
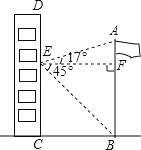
【题目】如图,在某次数学活动课中,小明为了测量校园内旗杆AB的高度,站在教学楼CD上的E处测得旗杆底端B的仰角∠BEF的度数为45°,测得旗杆顶端A的仰角∠AEF的度数为17°,旗杆底部B处与教学楼底部C处的水平距离BC为9m,求旗杆的高度(结果精确到0.1m).
【参考数据:sin17°=0.29,cos17°=0.96,tan17°=0.31】
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中,红色、黑色、白色的玻璃球共有60个,除颜色外其它完全相同,小明通过多次摸球试验后发现其中摸到红色,黑色球的概率稳定在15%和40%,则口袋中白色球的个数很可能是( )
A. 25 B. 26 C. 29 D. 27
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A∶∠B∶∠C=1∶1∶2,则△ABC的形状是( ).
A. 等腰三角形 B. 直角三角形 C. 等腰直角三角形 D. 等边三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com