
【题目】已知:在四边形 ABCD 中,∠A+∠C=180°,DB 平分∠ADC.
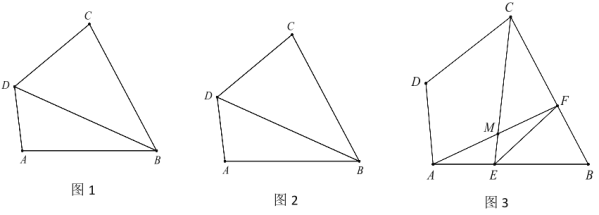
(1)如图 1求证:AB=BC
(2)如图 2,若∠ADB=60°,,试判断△ABC 的形状,并说明理由.
(3)如图 3,在(2)得条件下,在 AB 上取一点 E, BC 上取一点 F,连接 CE、AF 交于点 M,连接 EF,若∠CMF=60°,AD=EF=7,CD=8(CF﹥BF),求 AE 的长.
【答案】(1)见解析;(2)△ABC是等边三角形,理由见解析;(3)AE=5.
【解析】
(1)在DC上取一点H使DH=DA,易证△DAB≌△DHB,可得AB=HB,∠A=∠DHB,然后根据等角的补角相等以及等角对等边可得HB=BC,易证结论;
(2)连结AC,根据角平分线的定义和四边形内角和定理求出∠ABC =60°,即可得到△ABC是等边三角形;
(3)过点C作CN⊥AD交AD的延长线于点N,根据含30°直角三角形的性质求出DN=4,NC=![]() ,然后利用勾股定理求得AB= AC=13,由ASA证明△CAE≌△ABF,得到AE=BF,过点F作FK⊥AB,设BK=x,然后用含x的式子表示出FK和EK,在Rt△EFK中通过勾股定理列方程,求出x的值即可得解(注意舍去不合题意的解).
,然后利用勾股定理求得AB= AC=13,由ASA证明△CAE≌△ABF,得到AE=BF,过点F作FK⊥AB,设BK=x,然后用含x的式子表示出FK和EK,在Rt△EFK中通过勾股定理列方程,求出x的值即可得解(注意舍去不合题意的解).
解:(1)如图1,在DC上取一点H使DH=DA,
在△DAB和△DHB中,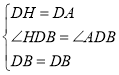 ,
,
∴△DAB≌△DHB(SAS),
∴AB=HB,∠A=∠DHB,
∵∠A+∠C=180°,∠DHB+∠BHC=180°,
∴∠C=∠BHC,
∴HB=BC,
∴AB=BC;
(2)△ABC是等边三角形,
理由:如图2,连结AC,
∵∠ADB=60°,∠A+∠C=180°,
∴∠ADC=120°,
∴∠ABC=180°-∠ADC=60°,
又由(1)得AB=BC,
∴△ABC是等边三角形;
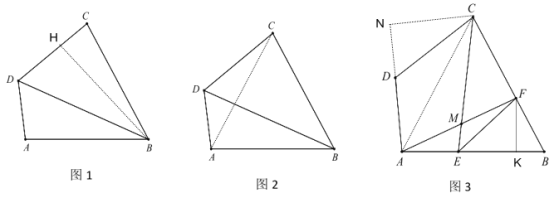
(3)过点C作CN⊥AD交AD的延长线于点N,
∵∠ADC=120°,CD=8,
∴∠NDC=60°,
∴DN=4,NC=![]() ,
,
∴AN=AD+DN=11,
∴AC=![]() ,
,
∴AB= AC=13,
∵∠ACE=∠CMF-∠CAM=60°-∠CAM,∠FAB=60°-∠CAM,
∴∠ACE=∠FAB,
在△CAE和△ABF中,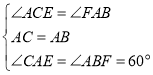 ,
,
∴△CAE≌△ABF(ASA),
∴AE=BF,
过点F作FK⊥AB,
设BK=x,则BF=2x,FK=![]() x,
x,
∴AE=BF=2x,
∴EK=AB-AE-BK=13-3x,
在Rt△EFK中,EF2=EK2+FK2,
∴72=(13-3x)2+(![]() x)2,
x)2,
解得:x1=![]() ,x2=4(舍去),
,x2=4(舍去),
∴AE=2x=5.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E,F分别在AD,DC上,且△BEF为等边三角形,下列结论:
①DE=DF;②∠AEB=75°;③BE=![]() DE;④AE+FC=EF.
DE;④AE+FC=EF.
其中正确的结论个数有( )
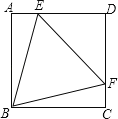
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】选择适当方法解下列方程:
(1)x2﹣4x+1=0(用配方法);
(2)3x(x﹣1)=2﹣2x
(3)(x﹣2)(x﹣3)=12
(4)2x2﹣2![]() x﹣5=0(公式法).
x﹣5=0(公式法).
查看答案和解析>>
科目:初中数学 来源: 题型:
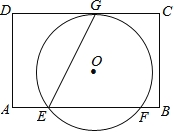
【题目】如图,在矩形ABCD中,AD=8,E是边AB上一点,且AE=![]() AB,⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线相交于另一点F,且EG:EF=
AB,⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线相交于另一点F,且EG:EF=![]() .当边AD或BC所在的直线与⊙O相切时,AB的长是 .
.当边AD或BC所在的直线与⊙O相切时,AB的长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名自行车运动员同时从A地出发到B地,在直线公路上进行骑自行车训练.如图,反映了甲、乙两名自行车运动员在公路上进行训练时的行驶路程S(千米)与行驶时间t(小时)之间的关系,下列四种说法:①甲的速度为40千米/小时;②乙的速度始终为50千米/小时;③行驶1小时时乙在甲前10千米;④3小时时甲追上乙.其中正确的个数有( )
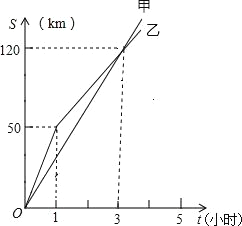
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:⊙O是△ABC的外接圆,点M为⊙O上一点.
(1)如图,若△ABC为等边三角形,BM=1,CM=2,求AM的长;

小明在解决这个问题时采用的方法是:延长MC到E,使ME=AM,从而可证△AME为等边三角形,并且△ABM≌△ACE,进而就可求出线段AM的长.
请你借鉴小明的方法写出AM的长,并写出推理过程.
(2)若△ABC为等腰直角三角形,∠BAC=90°,![]() ,(其中b>a),直接写出AM的长(用含有a,b的代数式表示).
,(其中b>a),直接写出AM的长(用含有a,b的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF;②△DEF是等边三角形;③△BEF是等腰三角形;④∠ADE=∠BEF,其中结论正确的个数是( )

A.3
B.4
C.1
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形AEHC是由三个全等矩形拼成的,AH与BE、BF、DF、DG、CG分别交于点P、Q、K、M、N.设△BPQ,△DKM,△CNH的面积依次为S1,S2,S3.若S1+S3=20,则S2的值为( )

A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+3与x轴交于点A(﹣1,0),B(3,0).
(1)求抛物线的解析式;
(2)过点D(0,![]() )作x轴的平行线交抛物线于E,F两点,求EF的长;
)作x轴的平行线交抛物线于E,F两点,求EF的长;
(3)当y≤![]() 时,直接写出x的取值范围是 .
时,直接写出x的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com