
【题目】选择适当方法解下列方程:
(1)x2﹣4x+1=0(用配方法);
(2)3x(x﹣1)=2﹣2x
(3)(x﹣2)(x﹣3)=12
(4)2x2﹣2![]() x﹣5=0(公式法).
x﹣5=0(公式法).
【答案】(1)x1=![]() ,x2=
,x2=![]() ; (2)x1=1; x2=﹣
; (2)x1=1; x2=﹣![]() ;(3)x1=6; x2=﹣1;(4)x1=
;(3)x1=6; x2=﹣1;(4)x1=![]() ; x2=
; x2=![]() .
.
【解析】
(1)利用配方法得到(x﹣2)2=3,然后利用直接开平方法解方程;
(2)先变形得到3x(x﹣1)+2(x﹣1)=0,然后利用因式分解法解方程;
(3)先把方程化为一般式,然后利用因式分解法解方程;
(4)利用求根公式法解方程.
解:(1)x2﹣4x=﹣1,
x2﹣4x+4=﹣1+4,
(x﹣2)2=3,
x﹣2=![]()
所以x1=![]() ,x2=
,x2=![]()
(2)3x(x﹣1)=2(1﹣x),
3x(x﹣1)+2(x﹣1)=0
(x﹣1)(3x+2)=0,
x﹣1=0或3x+2=0,
所以x1=1; x2=﹣![]() ;
;
(3)x2﹣5x+6=12,
x2﹣5x﹣6=0,
(x﹣6)(x+1)=0,
所以x1=6; x2=﹣1,
(4)解方程:2x2﹣2![]() x﹣5=0;
x﹣5=0;
x=
x1=![]() ; x2=
; x2=![]() .
.


科目:初中数学 来源: 题型:
【题目】《如果想毁掉一个孩子,就给他一部手机!》这是2017年微信圈一篇热传的文章.国际上,法国教育部宣布从 2018 年9月新学期起小学和初中禁止学生使用手机.为了解学生手机使用情况,某学校开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,②的 统计图,已知“查资料”的人数是 40人.请你根据以上信息解答下列问题:
(1)在扇形统计图中,“玩游戏”对应的百分比为______,圆心角度数是______度;
(2)补全条形统计图;
(3)该校共有学生2100人,估计每周使用手机时间在2 小时以上(不含2小时)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
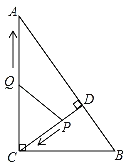
(1)求线段CD的长;
(2)当t为何值时,△CPQ与△ABC相似?
(3)是否存在某一时刻,使得PQ分△ACD的面积为2:3?若存在,求出t的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
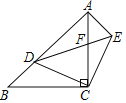
【题目】如图,在Rt△ACB中,∠ACB=90°,AC=BC,D是AB上的一个动点(不与点A,B重合),连接CD,将CD绕点C顺时针旋转90°得到CE,连接DE,DE与AC相交于点F,连接AE.下列结论:①△ACE≌△BCD;②若∠BCD=25°,则∠AED=65°;③DE2=2CFCA;④若AB=3![]() ,AD=2BD,则AF=
,AD=2BD,则AF=![]() .其中正确的结论是______.(填写所有正确结论的序号)
.其中正确的结论是______.(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M、N分别是斜边AB、DE的中点,点P为AD的中点,连接AE、BD.
(1)猜想PM与PN的数量关系及位置关系,请直接写出结论;
(2)现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP、BD分别交于点G、H.请判断(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;
(3)若图②中的等腰直角三角形变成直角三角形,使BC=kAC,CD=kCE,如图③,写出PM与PN的数量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
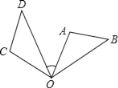
【题目】如图,将△OAB绕点O逆时针旋转80°得到△OCD,点A与点C是对应点.
(1)画出△OAB关于点O对称的图形(保留画图痕迹,不写画法);
(2)若∠A=110°,∠D=40°,求∠AOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC的一条边BC的长为5,另两边AB,AC的长分别为关于x的一元二次方程![]() 的两个实数根。
的两个实数根。
(1)求证:无论k为何值,方程总有两个不相等的实数根;
(2)当k=2时,请判断△ABC的形状并说明理由;
(3)k为何值时,△ABC是等腰三角形,并求△ABC的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在四边形 ABCD 中,∠A+∠C=180°,DB 平分∠ADC.
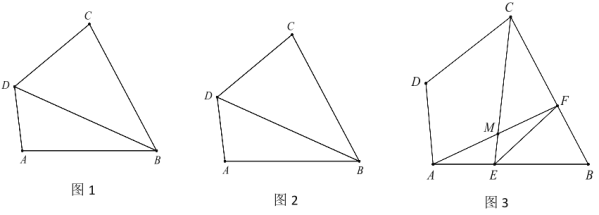
(1)如图 1求证:AB=BC
(2)如图 2,若∠ADB=60°,,试判断△ABC 的形状,并说明理由.
(3)如图 3,在(2)得条件下,在 AB 上取一点 E, BC 上取一点 F,连接 CE、AF 交于点 M,连接 EF,若∠CMF=60°,AD=EF=7,CD=8(CF﹥BF),求 AE 的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com