
【题目】如图,在Rt△ACB中,∠ACB=90°,AC=BC,D是AB上的一个动点(不与点A,B重合),连接CD,将CD绕点C顺时针旋转90°得到CE,连接DE,DE与AC相交于点F,连接AE.下列结论:①△ACE≌△BCD;②若∠BCD=25°,则∠AED=65°;③DE2=2CFCA;④若AB=3![]() ,AD=2BD,则AF=
,AD=2BD,则AF=![]() .其中正确的结论是______.(填写所有正确结论的序号)
.其中正确的结论是______.(填写所有正确结论的序号)
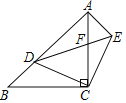
【答案】①②③
【解析】
先判断出∠BCD=∠ACE,即可判断出①正确;
先求出∠BDC=110°,进而得出∠AEC=110°,即可判断出②正确;
先判断出∠CAE=∠CEF,进而得出△CEF∽△CAE,即可得出CE2=CFAC,最后用勾股定理即可得出③正确;
先求出BC=AC=3,再求出BD=![]() ,进而求出CE=CD=
,进而求出CE=CD=![]() ,求出CF=
,求出CF=![]() ,即可判断出④错误.
,即可判断出④错误.
∵∠ACB=90°,
由旋转知,CD=CE,∠DCE=90°=∠ACB,
∴∠BCD=∠ACE,
在△BCD和△ACE中,
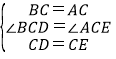 ,
,
∴△BCD≌△ACE,故①正确;
∵∠ACB=90°,BC=AC,
∴∠B=45°
∵∠BCD=25°,
∴∠BDC=180°-45°-25°=110°,
∵△BCD≌△ACE,
∴∠AEC=∠BDC=110°,
∵∠DCE=90°,CD=CE,
∴∠CED=45°,
则∠AED=∠AEC-∠CED=65°,故②正确;
∵△BCD≌△ACE,
∴∠CAE=∠CBD=45°=∠CEF,
∵∠ECF=∠ACE,
∴△CEF∽△CAE,
∴![]() ,
,
∴CE2=CFAC,
在等腰直角三角形CDE中,DE2=2CE2=2CFAC,故③正确;
如图,过点D作DG⊥BC于G,
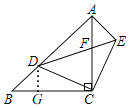
∵AB=3![]() ,
,
∴AC=BC=3,
∵AD=2BD,
∴BD=![]() AB=
AB=![]() ,
,
∴DG=BG=1,
∴CG=BC-BG=3-1=2,
在Rt△CDG中,根据勾股定理得,CD=![]() ,
,
∵△BCD≌△ACE,
∴CE=![]() ,
,
∵CE2=CFAC,
∴CF=![]() ,
,
∴AF=AC-CF=3-![]() =
=![]() ,故④错误,
,故④错误,
故答案为:①②③.


 教学练新同步练习系列答案
教学练新同步练习系列答案科目:初中数学 来源: 题型:
【题目】用一段长32m的篱笆和长8m的墙,围成一个矩形的菜园.
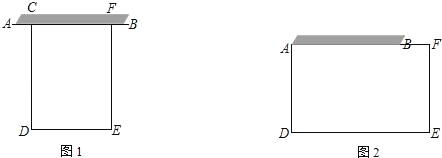
(1)如图1,如果矩形菜园的一边靠墙AB,另三边由篱笆CDEF围成
①设DE等于xm,直接写出菜园面积y与x之间的函数关系式,并写出自变量的取值范围;
②菜园的面积能不能等于110m2?若能,求出此时x的值;若不能,请说明理由;
(2)如图2,如果矩形菜园的一边由墙AB和一节篱笆BF构成,另三边由篱笆ADEF围成,求菜园面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,二次函数 y=(x+2)2 的图象与 x 轴交于点 A,与 y 轴交于点 B.
(1)求点 A、点 B 的坐标;
(2)求 S△AOB;
(3)求对称轴方程;
(4)在对称轴上是否存在一点P,使以 P,A,O,B 为顶点的四边形为平行四边形?若存在,求P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC平分∠DAB,AC2=ABAD,∠ADC=90°,E为AB的中点.

(1)求证:△ADC∽△ACB;
(2)CE与AD有怎样的位置关系?试说明理由;
(3)若AD=4,AB=6,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
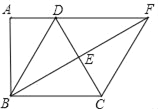
【题目】如图,四边形ABCD中,∠A=90°,AD∥BC,BE⊥CD于E交AD的延长线于F,DC=2AD,AB=BE.
(1)求证:AD=DE.
(2)求证:四边形BCFD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
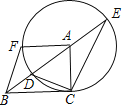
【题目】如图,在Rt△ACB中,∠ACB=90°,以点A为圆心,AC长为半径的圆交AB于点D,BA的延长线交⊙A于点E,连接CE,CD,F是⊙A上一点,点F与点C位于BE两侧,且∠FAB=∠ABC,连接BF.
(1)求证:∠BCD=∠BEC;
(2)若BC=2,BD=1,求CE的长及sin∠ABF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有除颜色外其余均相同的5个小球,其中红球3个,黑球2个.
(1)若先从袋中取出x(x>0)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,若A为必然事件,则x的值为 ;
(2)若从袋中随机摸出2个球,正好红球、黑球各1个,用画树状图或列表法求这个事件的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区商店以2元的批发价进了一批纪念品.经调查发现,每个定价3元,每天可以能卖出500件,而且定价每上涨0.1元,其销售量将减少10件.根据规定:纪念品售价不能超过批发价的2.5倍.
(1)当每个纪念品定价为3.5元时,商店每天能卖出________件;
(2)如果商店要实现每天800元的销售利润,那该如何定价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学对本校初2017届500名学生中中考参加体育加试测试情况进行调查,根据男生1000米及女生800米测试成绩整理,绘制成不完整的统计图,(图①,图②),请根据统计图提供的信息,回答下列问题:
(1)该校毕业生中男生有 人;扇形统计图中a= ;

(2)补全条形统计图;
(3)若500名学生中随机抽取一名学生,这名学生该项成绩在8分及8分以下的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com