
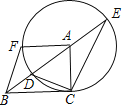
【题目】如图,在Rt△ACB中,∠ACB=90°,以点A为圆心,AC长为半径的圆交AB于点D,BA的延长线交⊙A于点E,连接CE,CD,F是⊙A上一点,点F与点C位于BE两侧,且∠FAB=∠ABC,连接BF.
(1)求证:∠BCD=∠BEC;
(2)若BC=2,BD=1,求CE的长及sin∠ABF的值.
【答案】(1)见解析;(2)CE=![]() , sin∠ABF=
, sin∠ABF=![]() .
.
【解析】
(1)先利用等角的余角相等即可得出结论;
(2)先判断出△BDC∽△BCE得出比例式求出BE=4,DE=3,利用勾股定理求出CD,CE,再判断出△AFM∽△BAC,进而判断出四边形FNCA是矩形,求出FN,NC,即:BN,再用勾股定理求出BF,即可得出结论.
(1)∵∠ACB=90°,
∴∠BCD+∠ACD=90°,
∵DE是⊙A的直径,
∴∠DCE=90°,
∴∠BEC+∠CDE=90°,
∵AD=AC,
∴∠CDE=∠ACD,
∴∠BCD=∠BEC,
(2)∵∠BCD=∠BEC,∠EBC=∠EBC,
∴△BDC∽△BCE,
∴![]() ,
,
∵BC=2,BD=1,
∴BE=4,EC=2CD,
∴DE=BE﹣BD=3,
在Rt△DCE中,DE2=CD2+CE2=9,
∴CD=![]() ,CE=
,CE=![]() ,
,
过点F作FM⊥AB于M,
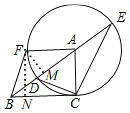
∵∠FAB=∠ABC,∠FMA=∠ACB=90°,
∴△AFM∽△BAC,
∴![]() ,
,
∵DE=3,
∴AD=AF=AC=![]() ,AB=
,AB=![]() ,
,
∴FM=![]() ,
,
过点F作FN⊥BC于N,
∴∠FNC=90°,
∵∠FAB=∠ABC,
∴FA∥BC,
∴∠FAC=∠ACB=90°,
∴四边形FNCA是矩形,
∴FN=AC=![]() ,NC=AF=
,NC=AF=![]() ,
,
∴BN=![]() ,
,
在Rt△FBN中,BF=![]() ,
,
在Rt△FBM中,sin∠ABF=![]() .
.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
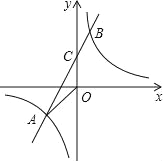
【题目】如图,已知A(n,﹣2),B(1,4)是一次函数y=kx+b的图象与反比例函数y=![]() 的图象的两个交点,直线AB与y轴交于点C.
的图象的两个交点,直线AB与y轴交于点C.
(1)求反比例函数和一次函数的解析式;
(2)求△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物流公司要把3000吨货物从M市运到W市.(每日的运输量为固定值)
(1)从运输开始,每天运输的货物吨数y(单位:吨)与运输时间x(单位:天)之间有怎样的函数关系式?
(2)因受到沿线道路改扩建工程影响,实际每天的运输量比原计划少20%,以致推迟1天完成运输任务,求原计划完成运输任务的天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学兴趣小组研究某型号冷柜温度的变化情况,发现该冷柜的工作过程是:当温度达到设定温度![]() ℃时,制冷停止,此后冷柜中的温度开始逐渐上升,当上升到
℃时,制冷停止,此后冷柜中的温度开始逐渐上升,当上升到![]() ℃时,制冷开始,温度开始逐渐下降,当冷柜自动制冷至
℃时,制冷开始,温度开始逐渐下降,当冷柜自动制冷至![]() ℃时,制冷再次停止,…,按照以上方式循环进行.同学们记录
℃时,制冷再次停止,…,按照以上方式循环进行.同学们记录![]() 内9个时间点冷柜中的温度
内9个时间点冷柜中的温度![]() (℃)随时间
(℃)随时间![]() 变化情况,制成下表:
变化情况,制成下表:
时间 | … | 4 | 8 | 10 | 16 | 20 | 21 | 22 | 23 | 24 | … |
温度 | … |
|
|
|
|
|
|
|
|
| … |
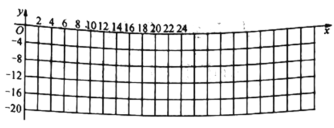
(1)如图,在直角坐标系中,描出上表数据对应的点,并画出当![]() 时温度
时温度![]() 随时间
随时间![]() 变化的函数图象;
变化的函数图象;
(2)通过图表分析发现,冷柜中的温度![]() 是时间
是时间![]() 的函数.
的函数.
①当![]() 时,写出符合表中数据的函数解析式;
时,写出符合表中数据的函数解析式;
②当![]() 时,写出符合表中数据的函数解析式;
时,写出符合表中数据的函数解析式;
(3)当前冷柜的温度![]() ℃时,冷柜继续工作36分钟,此时冷柜中的温度是多少?
℃时,冷柜继续工作36分钟,此时冷柜中的温度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
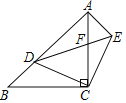
【题目】如图,在Rt△ACB中,∠ACB=90°,AC=BC,D是AB上的一个动点(不与点A,B重合),连接CD,将CD绕点C顺时针旋转90°得到CE,连接DE,DE与AC相交于点F,连接AE.下列结论:①△ACE≌△BCD;②若∠BCD=25°,则∠AED=65°;③DE2=2CFCA;④若AB=3![]() ,AD=2BD,则AF=
,AD=2BD,则AF=![]() .其中正确的结论是______.(填写所有正确结论的序号)
.其中正确的结论是______.(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() 是
是![]() 边上一点,
边上一点,![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 边上的动点,且始终保持
边上的动点,且始终保持![]() .
.


(1)求![]() 的长;
的长;
(2)若四边形![]() 为平行四边形时,求
为平行四边形时,求![]() 的周长;
的周长;
(3)将![]() 沿它的一条边翻折,当翻折前后两个三角形组成的四边形为菱形时,求线段
沿它的一条边翻折,当翻折前后两个三角形组成的四边形为菱形时,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
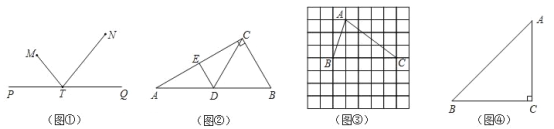
【题目】如图①,直线PQ同侧有两点M,N,点T在直线PQ上,若∠MTP=∠NTQ,则称点T为M,N在直线PQ上的投射点.
(1)如图②,在Rt△ABC中,∠B=60°,D为斜边AB的中点,E为AC的中点.求证:点D为C,E在直线AB上的投射点;
(2)如图③,在正方形网格中,已知点A,B,C三点均在格点上,请仅用没有刻度的直尺在AC上画出点P,在BC上画出点Q,使A,P在BC上的投射点Q满足CQ=2BQ;
(3)如图④,在Rt△ABC中,∠C=90°,AC=BC,在AB,BC边上是否分别存在点D,E,使点D为E,C在AB上的投射点,点E为A,D在BC上的投射点?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
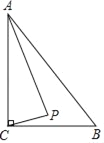
【题目】如图,在Rt△ABC 中,∠ACB=90°,AC=6,BC=4,点P是△ABC内部的一个动点,且满足∠PAC=∠PCB,则线段BP长的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=(x-3)2+k的图象过A(-1,y1)、B(2,y2)、C(3+![]() ,y3)三点,则y1、y2、y3的大小关系正确的是( )
,y3)三点,则y1、y2、y3的大小关系正确的是( )
A. y1>y2>y3 B. y2>y1>y3 C. y1>y3>y2 D. y3>y1>y2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com