
【题目】已知△ABC的一条边BC的长为5,另两边AB,AC的长分别为关于x的一元二次方程![]() 的两个实数根。
的两个实数根。
(1)求证:无论k为何值,方程总有两个不相等的实数根;
(2)当k=2时,请判断△ABC的形状并说明理由;
(3)k为何值时,△ABC是等腰三角形,并求△ABC的周长。
【答案】(1)见解析;(2)△ABC为直角三角形,见解析;(3)当k=4时,△ABC是等腰三角形,△ABC的周长=16;当k=3时,△ABC是等腰三角形,△ABC的周长=14.
【解析】
(1)根据根的判别式即可求出答案;
(2)将k的值代入原方程并求解后,根据勾股定理逆定理即可求出答案;
(3)根据等腰三角形的性质即可求出k的值.
(1)△=(2k+3)2-4(k2+3k+2)=1>0,
∴无论k为何值,方程总有两个不相等的实数根;
(2)当k=2时,
∴原方程化为:x2-7x+12=0,
解得:x=3或x=4,
∴32+42=52,
∴△ABC是直角三角形;
(3)当BC是等腰三角形的腰时,
∴x=5是方程的x2-(2k+3)x+k2+3k+2=0解,
∴25-5(2k+3)+k2+3k+2=0,
解得:k2-7k+12=0,
∴k=3或k=4,
若k=3时,
则方程为:x2-9x+20=0,
∴x=4或x=5,满足三角形三边关系,
此时周长为14;
若k=4时,
则方程:x2-11x+30=0,
∴x=5或x=6,满足三角形三边关系,
此时周长为16;
当BC是等腰三角形的底边时,
此时方程的x2-(2k+3)x+k2+3k+2=0有两个相等的解,不满足题意,
综上所述,△ABC的周长为14或16.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y1=![]() x2-2x,直线y2=-2x+b相交于A,B两点,其中点A的横坐标为2.当x任取一值时,x对应的函数值分别为y1,y2,取m=
x2-2x,直线y2=-2x+b相交于A,B两点,其中点A的横坐标为2.当x任取一值时,x对应的函数值分别为y1,y2,取m=![]() (|y1-y2|+y1+y2).则
(|y1-y2|+y1+y2).则

A. 当x<-2时,m=y2.B. m随x的增大而减小.
C. 当m=2时,x=0.D. m≥-2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一路灯距地面6.4米,身高1.6米的小方从距离灯的底部(点O)5米的A处,沿OA所在的直线行走到点C时,人影长度增长3米,

求:(1)小方在A处时的影子AB的长;(2)小方行走的路程AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】选择适当方法解下列方程:
(1)x2﹣4x+1=0(用配方法);
(2)3x(x﹣1)=2﹣2x
(3)(x﹣2)(x﹣3)=12
(4)2x2﹣2![]() x﹣5=0(公式法).
x﹣5=0(公式法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,∠A是锐角,E为边AD上一点,△ABE沿着BE折叠,使点A的对应点F恰好落在边CD上,连接EF,BF,给出下列结论:
①若∠A=70°,则∠ABE=35°;②若点F是CD的中点,则S△ABE![]() S菱形ABCD
S菱形ABCD
下列判断正确的是( )

A. ①,②都对B. ①,②都错C. ①对,②错D. ①错,②对
查看答案和解析>>
科目:初中数学 来源: 题型:
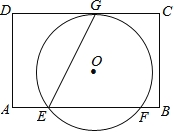
【题目】如图,在矩形ABCD中,AD=8,E是边AB上一点,且AE=![]() AB,⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线相交于另一点F,且EG:EF=
AB,⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线相交于另一点F,且EG:EF=![]() .当边AD或BC所在的直线与⊙O相切时,AB的长是 .
.当边AD或BC所在的直线与⊙O相切时,AB的长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名自行车运动员同时从A地出发到B地,在直线公路上进行骑自行车训练.如图,反映了甲、乙两名自行车运动员在公路上进行训练时的行驶路程S(千米)与行驶时间t(小时)之间的关系,下列四种说法:①甲的速度为40千米/小时;②乙的速度始终为50千米/小时;③行驶1小时时乙在甲前10千米;④3小时时甲追上乙.其中正确的个数有( )
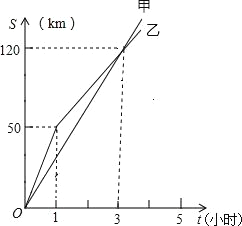
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF;②△DEF是等边三角形;③△BEF是等腰三角形;④∠ADE=∠BEF,其中结论正确的个数是( )

A.3
B.4
C.1
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(k﹣1)x2+(2k﹣3)x+k+1=0有两个不相等的实数根.
(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程x2﹣4x+k=0与x2+mx﹣1=0有一个相同的根,求此时m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com