
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
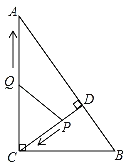
(1)求线段CD的长;
(2)当t为何值时,△CPQ与△ABC相似?
(3)是否存在某一时刻,使得PQ分△ACD的面积为2:3?若存在,求出t的值,若不存在,请说明理由.
【答案】(1)CD=![]() ;(2)t为3秒或
;(2)t为3秒或![]() 秒时,△CPQ与△ABC相似;(3)不存在,见解析.
秒时,△CPQ与△ABC相似;(3)不存在,见解析.
【解析】
(1)先利用勾股定理求出AB=10,进利用面积法求出CD;
(2)先表示出CP,再判断出∠ACD=∠B,进而分两种情况,利用相似三角形得出比例式建立方程求解,即可得出结论;
(3)先判断出△CEQ∽△CDA,得出![]() ,进而表示出QE=
,进而表示出QE=![]() t,再分当S△CPQ=
t,再分当S△CPQ=![]() S△ACD时,和当S△CPD=
S△ACD时,和当S△CPD=![]() S△ACD时,利用面积建立方程求解即可得出结论.
S△ACD时,利用面积建立方程求解即可得出结论.
解:(1)在Rt△ABC中,根据勾股定理得,AB=![]() =
=![]() =10,
=10,
∵S△ABC=![]() ACBC=
ACBC=![]() ABCD,
ABCD,
∴CD=![]() =
=![]() =
=![]() ,
,
(2)由(1)知,CD=![]() ,
,
由运动知,CQ=t,DP=t,
∴CP=CD﹣DP=![]() ﹣t,
﹣t,
∵∠ACB=90°,
∴∠ACD+∠BCD=90°,
∵CD⊥AB,
∴∠B+∠BCD=90°,
∴∠ACD=∠B,
∵△CPQ与△ABC相似,
∴①△CPQ∽△BCA,
∴![]() ,
,
∴ ,
,
∴t=3
②△CPQ∽△BAC,
∴![]() ,
,
∴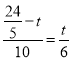
∴t=![]() ,
,
即:t为3秒或![]() 秒时,△CPQ与△ABC相似;
秒时,△CPQ与△ABC相似;
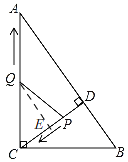
(3)假设存在,如图,
在Rt△ACD中,根据勾股定理得,AD=![]() =
= =
=![]() ,
,
过点Q作CE⊥CD于E,
∴QE∥AD,
∴△CEQ∽△CDA,
∴![]() ,
,
∴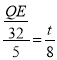 ,
,
∴QE=![]() t,
t,
∵S△CPQ=![]() CPQE=
CPQE=![]() (
(![]() ﹣t)
﹣t)![]() t,
t,
∴S△ACD=![]() ADCD=
ADCD=![]() ×
×![]() ×
×![]() ,
,
∵PQ分△ACD的面积为2:3,
∴①当S△CPQ=![]() S△ACD时,
S△ACD时,
∴![]() (
(![]() ﹣t)
﹣t)![]() t=
t=![]() ×
×![]() ×
×![]() ×
×![]() ,
,
∴25t2﹣120t+384=0而△=1202﹣4×25×384=14400﹣38400<0,
此方程无解,即:此种情况不存在,
②当S△CPD=![]() S△ACD时,
S△ACD时,![]() (
(![]() ﹣t)
﹣t)![]() t=
t=![]() ×
×![]() ×
×![]() ×
×![]() ,
,
∴25t2﹣120t+576=0,而△=1202﹣4×25×576=14400﹣57600<0,
此方程无解,即:此种情况不存在,
即:不存在某时刻,使得PQ分△ACD的面积为2:3.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直坐标系中,有A(﹣2,3),B(﹣2,﹣1)两点,若点A关于y轴的对称点为点C,点B向右平移8个单位到点D.
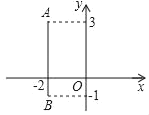
(1)分别写出点C,点D的坐标;
(2)若一次函数图象经过C,D两点,求一次函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y1=![]() x2-2x,直线y2=-2x+b相交于A,B两点,其中点A的横坐标为2.当x任取一值时,x对应的函数值分别为y1,y2,取m=
x2-2x,直线y2=-2x+b相交于A,B两点,其中点A的横坐标为2.当x任取一值时,x对应的函数值分别为y1,y2,取m=![]() (|y1-y2|+y1+y2).则
(|y1-y2|+y1+y2).则

A. 当x<-2时,m=y2.B. m随x的增大而减小.
C. 当m=2时,x=0.D. m≥-2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E,F分别在AD,DC上,且△BEF为等边三角形,下列结论:
①DE=DF;②∠AEB=75°;③BE=![]() DE;④AE+FC=EF.
DE;④AE+FC=EF.
其中正确的结论个数有( )
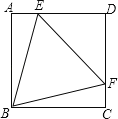
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解下列方程:
(1)x2﹣3x﹣2=0;(2)x2﹣2![]() x+2=0;(3)3x(x﹣2)=5(2﹣x);(4)x2﹣(2m+1)x+m2+m=0
x+2=0;(3)3x(x﹣2)=5(2﹣x);(4)x2﹣(2m+1)x+m2+m=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点P是AB边上一点![]() 不与A,B重合
不与A,B重合![]() ,
,![]() ,过点作
,过点作![]() ,交AD边于点Q,连结CQ.
,交AD边于点Q,连结CQ.
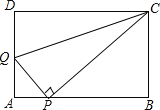
![]() 若
若![]() ,求证:四边形ABCD是矩形;
,求证:四边形ABCD是矩形;
![]() 在
在![]() 的条件下,当
的条件下,当![]() ,
,![]() 时,求AQ的长.
时,求AQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一路灯距地面6.4米,身高1.6米的小方从距离灯的底部(点O)5米的A处,沿OA所在的直线行走到点C时,人影长度增长3米,

求:(1)小方在A处时的影子AB的长;(2)小方行走的路程AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】选择适当方法解下列方程:
(1)x2﹣4x+1=0(用配方法);
(2)3x(x﹣1)=2﹣2x
(3)(x﹣2)(x﹣3)=12
(4)2x2﹣2![]() x﹣5=0(公式法).
x﹣5=0(公式法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF;②△DEF是等边三角形;③△BEF是等腰三角形;④∠ADE=∠BEF,其中结论正确的个数是( )

A.3
B.4
C.1
D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com