
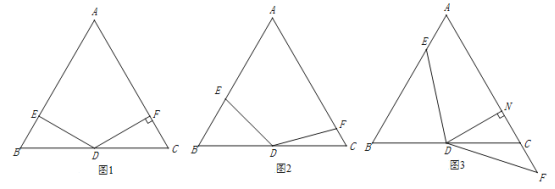
【题目】在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E,DF与线段AC(或AC的延长线)相交于点F.
(1)如图1,若DF⊥AC,垂足为F,AB=4,求BE的长;
(2)如图2,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF扔与线段AC相交于点F.求证:![]() ;
;
(3)如图3,将(2)中的∠EDF继续绕点D顺时针旋转一定的角度,使DF与线段AC的延长线交与点F,作DN⊥AC于点N,若DN=FN,求证:![]() .
.
【答案】2;见解析;见解析.
【解析】
试题根据四边形的内角和定理得出DE⊥AB,从而得到BE的长度;取AB的中点G,连接DG,得出DG为△ABC的中位线,则DG=DC,∠BGD=∠C=60°,根据四边形对角互补得出∠GED=∠DFC,从而得到△DEG和△DFC全等,得到EG=CF,得出答案;取AB的中点G,连接DG,同⑵,易证△DEG≌△DFC得出EG=CF,设CN=x,根据Rt△DCN得出CD=2x,DN=![]() x,根据题意得出EG、BE与x的关系,从而进行说明.
x,根据题意得出EG、BE与x的关系,从而进行说明.
试题解析:(1)、由四边形AEDF的内角和为![]() ,可知DE⊥AB,故BE=2
,可知DE⊥AB,故BE=2
(2)、取AB的中点G,连接DG 易证:DG为△ABC的中位线,故DG=DC,∠BGD=∠C=60°
又四边形AEDF的对角互补,故∠GED=∠DFC ∴△DEG≌△DFC 故EG=CF
∴BE+CF=BE+EG=BG=![]() AB
AB
(3)、取AB的中点G,连接DG 同⑵,易证△DEG≌△DFC 故EG=CF
故BE-CF=BE-EG=BG=![]() 设
设![]() 在Rt△DCN中,CD=2x,DN=
在Rt△DCN中,CD=2x,DN=![]()
在RT△DFN中,NF=DN=![]() ,故EG=CF=
,故EG=CF=![]() BE=BG+EG=DC+CF=2x+
BE=BG+EG=DC+CF=2x+![]() =
=![]()
故BE+CF=![]()
![]()
故![]()


科目:初中数学 来源: 题型:
【题目】如图所示的港珠澳大桥是目前桥梁设计中广泛采用的斜拉桥,它用粗大的钢索将桥面拉住,为检测钢索的抗拉强度,桥梁建设方从甲、乙两家生产钢索的厂方各随机选取5根钢索进行抗拉强度的检测,数据统计如下(单位:百吨)

甲、乙两厂钢索抗拉强度检测统计表
钢索 | 1 | 2 | 3 | 4 | 5 | 平均数 | 中位数 | 方差 |
甲厂 | 10 | 11 | 9 | 10 | 12 | 10.4 | 10 | 1.04 |
乙厂 | 10 | 8 | 12 | 7 | 13 | a | b | c |
(1)求乙厂5根钢索抗拉强度的平均数a(百吨)、中位数b(百吨)和方差c(平方百吨).
(2)桥梁建设方决定从抗拉强度的总体水平和稳定性来决定钢索的质量,问哪一家的钢索质量更优?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电子厂商设计了一款制造成本为18元新型电子厂品,投放市场进行试销.经过调查,得到每月销售量y(万件)与销售单价x(元)之间的部分数据如下:
销售单价x(元/件) | … | 20 | 25 | 30 | 35 | … |
每月销售量y(万件) | … | 60 | 50 | 40 | 30 | … |
(1)求出每月销售量y(万件)与销售单价x(元)之间的函数关系式.
(2)求出每月的利润z(万元)与销售单x(元)之间的函数关系式.
(3)根据相关部门规定,这种电子产品的销售利润率不能高于50%,而且该电子厂制造出这种产品每月的制造成本不能超过900万元.那么并求出当销售单价定为多少元时,厂商每月能获得最大利润?最大利润是多少?(利润=售价﹣制造成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上学习了圆周角的概念和性质:“顶点在圆上,两边与圆相交”,“同弧所对的圆周角相等”,小明在课后继续对圆外角和圆内角进行了探究.
下面是他的探究过程,请补充完整:
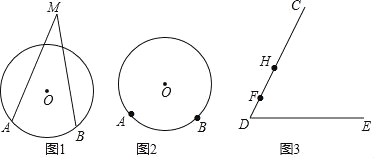
定义概念:顶点在圆外,两边与圆相交的角叫做圆外角,顶点在圆内,两边与圆相交的角叫做圆内角.如图1,∠M为![]() 所对的一个圆外角.
所对的一个圆外角.
(1)请在图2中画出![]() 所对的一个圆内角;
所对的一个圆内角;
提出猜想
(2)通过多次画图、测量,获得了两个猜想:一条弧所对的圆外角______这条弧所对的圆周角;一条弧所对的圆内角______这条弧所对的圆周角;(填“大于”、“等于”或“小于”)
推理证明:
(3)利用图1或图2,在以上两个猜想中任选一个进行证明;
问题解决
经过证明后,上述两个猜想都是正确的,继续探究发现,还可以解决下面的问题.
(4)如图3,F,H是∠CDE的边DC上两点,在边DE上找一点P使得∠FPH最大.请简述如何确定点P的位置.(写出思路即可,不要求写出作法和画图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生的安全意识情况,在全校范围内随机抽取部分学生进行问卷调查,根据调查结果,把学生的安全意识分成“淡薄”、“一般”、“较强”、“很强”四个层次,并绘制成如下两幅尚不完整的统计图.

根据以上信息,解答下列问题:
(1)这次调查一共抽取了 名学生,其中安全意识为“很强”的学生占被调查学生总数的百分比是 ;
(2)请将条形统计图补充完整;
(3)该校有1800名学生,现要对安全意识为“淡薄”、“一般”的学生强化安全教育,根据调查结果,估计全校需要强化安全教育的学生约有 名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向的B处,求此时轮船所在的B处与灯塔P的距离.(参考数据:![]() ≈2.449,结果保留整数)
≈2.449,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形的一条边长为x,周长的一半为y,定义(x,y)为这个矩形的坐标。如图2,在平面直角坐标系中,直线x=1,y=3将第一象限划分成4个区域,已知矩形1的坐标的对应点A落在如图所示的双曲线上,矩形2的坐标的对应点落在区域④中,则下面叙述中正确的是( )

A. 点A的横坐标有可能大于3
B. 矩形1是正方形时,点A位于区域②
C. 当点A沿双曲线向上移动时,矩形1的面积减小
D. 当点A位于区域①时,矩形1可能和矩形2全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】跳绳是大家喜闻乐见的一项体育运动,集体跳绳时,需要两人同频甩动绳子,当绳子甩到最高处时,其形状可近似看作抛物线,下图是小明和小亮甩绳子到最高处时的示意图,两人拿绳子的手之间的距离为4![]() ,离地面的高度为1
,离地面的高度为1![]() ,以小明的手所在位置为原点建立平面直角坐标系.
,以小明的手所在位置为原点建立平面直角坐标系.
(1)当身高为15![]() 的小红站在绳子的正下方,且距小明拿绳子手的右侧1
的小红站在绳子的正下方,且距小明拿绳子手的右侧1![]() 处时,绳子刚好通过小红的头顶,求绳子所对应的抛物线的表达式;
处时,绳子刚好通过小红的头顶,求绳子所对应的抛物线的表达式;
(2)若身高为![]() 的小丽也站在绳子的正下方.
的小丽也站在绳子的正下方.
①当小丽在距小亮拿绳子手的左侧1.5![]() 处时,绳子能碰到小丽的头吗?请说明理由;
处时,绳子能碰到小丽的头吗?请说明理由;
②设小丽与小亮拿绳子手之间的水平距离为![]() ,为保证绳子不碰到小丽的头顶,求
,为保证绳子不碰到小丽的头顶,求![]() 的取值范围.(参考数据:
的取值范围.(参考数据: ![]() 取3.16)
取3.16)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象经过点
的图象经过点![]() ,直线
,直线![]() 与x轴交于点
与x轴交于点![]() .
.
(1)求![]() 的值;
的值;
(2)过第二象限的点![]() 作平行于x轴的直线,交直线
作平行于x轴的直线,交直线![]() 于点C,交函数
于点C,交函数![]() 的图象于点D.
的图象于点D.
①当![]() 时,判断线段PD与PC的数量关系,并说明理由;
时,判断线段PD与PC的数量关系,并说明理由;
②若![]() ,结合函数的图象,直接写出n的取值范围.
,结合函数的图象,直接写出n的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com