
����Ŀ��ij���ӳ��������һ������ɱ�Ϊ18Ԫ���͵��ӳ�Ʒ��Ͷ���г������������������飬�õ�ÿ��������y������������۵���x��Ԫ��֮��IJ����������£�
���۵���x��Ԫ/���� | �� | 20 | 25 | 30 | 35 | �� |
ÿ��������y������� | �� | 60 | 50 | 40 | 30 | �� |
��1�����ÿ��������y������������۵���x��Ԫ��֮��ĺ�����ϵʽ��
��2�����ÿ�µ�����z����Ԫ�������۵�x��Ԫ��֮��ĺ�����ϵʽ��
��3��������ز��Ź涨�����ֵ��Ӳ�Ʒ�����������ʲ��ܸ���50%�����Ҹõ��ӳ���������ֲ�Ʒÿ�µ�����ɱ����ܳ���900��Ԫ����ô����������۵��۶�Ϊ����Ԫʱ������ÿ���ܻ�����������������Ƕ��٣�������=�ۼ۩�����ɱ���
���𰸡���1��y=��2x+100����2��z=��2x2+136x��1800����3�������۵���Ϊ27Ԫʱ������ÿ�»�õ���������������Ϊ404��Ԫ.
��������������(1)�������躯������ʽΪy=kx+b��Ȼ�����ô���ϵ���������������ʽ��(2)������������=��������������ó���������ʽ��(3)�����ȸ��ݳɱ�������900��Ԫ�ó�x��ȡֵ��Χ���������������ʲ��ܸ���50%�ó�x��ȡֵ��Χ��Ȼ���κ��������䷽�ɶ���ʽ�������ݶ��κ��������ʵó����ֵ��
��⣺(1)���⣺��������y������������۵���x��Ԫ��֮��ĺ�����ϵʽΪ��y=kx+b��
�ѣ�20��60������30��40������y=kx+b��![]() ����ã�
����ã�![]() ��
��
��ÿ��������y������������۵���x��Ԫ��֮��ĺ�����ϵʽΪ��y=��2x+100��
(2)���⣺������ã�z=y��x��18��=����2x+100����x��18��=��2x2+136x��1800��
��3���⣺�߳���ÿ�µ�����ɱ�������900��Ԫ��ÿ������ɱ�Ϊ18Ԫ��
��ÿ�µ�������Ϊ��С�ڵ���![]() =50�����y=��2x+100��50�� ��ã�x��25��
=50�����y=��2x+100��50�� ��ã�x��25��
�������������ʲ��ܸ���50%����25��x��27��
��z=��2x2+136x��1800=��2��x��34��2+512��
��ͼ�����£��Գ������z��x����������� ��x=27ʱ��z���Ϊ��404��Ԫ��
�����۵���Ϊ27Ԫʱ������ÿ�»�õ���������������Ϊ404��Ԫ.


 ϰ�⾫ѡϵ�д�
ϰ�⾫ѡϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У�AC��BC��2������ABC�Ƶ�A��ʱ����ת60�㣬����BD����ͼ����Ӱ���ֵ�����ǣ�������
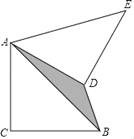
A. 2![]() ��2B. 2
��2B. 2![]() C.
C. ![]() ��1D. 4
��1D. 4![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У���C=90�㣬��BAC=60�㣬��ABC�Ƶ�C˳ʱ����ת����ת��Ϊ����0�㣼����180��������A��B�Ķ�Ӧ��ֱ��ǵ�D��E��
��1����ͼ1������Dǡ�����ڱ�AB��ʱ�����ж�DE��AC��λ�ù�ϵ����˵�����ɣ�
��2����ͼ2������B��D��E����ǡ����һֱ����ʱ����ת����=__������ʱֱ��CE��AB��λ�ù�ϵ��__��
��3���ڣ�2���������£�����AE������BDC�����S1����AEC�����S2����S1��S2��������ϵ��_____��
��4����ͼ3������B��D��E���㲻��һֱ����ʱ����3���е�S1��S2��������ϵ��Ȼ��������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
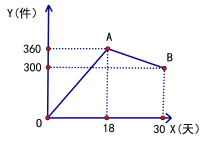
����Ŀ��ij�̳Ǿ���һ���²�Ʒ���ò�Ʒ�Ľ���6Ԫ/�����ۼ�Ϊ9Ԫ/��.������Ա��30������������и��ټ�¼�����Ƴ�ͼ��ͼ�е�����OAB��ʾ��������![]() ������������ʱ��
������������ʱ��![]() ���죩֮��ĺ�����ϵ.
���죩֮��ĺ�����ϵ.
��1����18������������� ��
��2����![]() ��
��![]() ֮��ĺ�����ϵʽ����д��
֮��ĺ�����ϵʽ����д��![]() ��ȡֵ��Χ
��ȡֵ��Χ
��3��������������900Ԫ���������ж����죿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һֻ�����������ﹲ��3��������2������1���������dz���ɫ�����ͬ��
��1�����������������һ�����ǰ���ĸ�����
��2�����������������һ����¼����ɫ�����Ż����ӣ����Ⱥ�������һ�������������������ǰ���ĸ��ʣ���������״ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����У�μ���ѧ��������У�μӳ�����������ȣ�������������ѧ���ɼ��ֱ�Ϊ 70 �֡�80 �֡�90 �֡�100 �֣�����ͳ�����ݻ����������в�������ͳ��ͼ����
��У�ɼ�ͳ�Ʊ���
���� | 70 �� | 80 �� | 90 �� | 100 �� |
���� | 11 | 0 | 8 |

(1)��ͼ 1 �У���80 �������ڵ����ε�Բ�Ľǵ��� �ȣ�
(2)�뽫��У�ɼ�ͳ�Ʊ���ͼ 2 ����У�ɼ�����ͳ��ͼ����������
(3)������У��ƽ���ֺͼ�У����λ����
(4)����ؽ�����Ҫ��֯ 8 �˵Ĵ����Ӳμ��м�����������������Ϊ�˱��ڹ�����������������ѧУ�е�һ����ѡ����ѡ�֣�����ΪӦѡ�ĸ�ѧУ�����Ҫ˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ҹ涨���˷������¡�����ͼ�����ø�ѵ���˰���㷽���ǣ�
�ٸ�Ѳ�����800Ԫ�IJ���˰��
�ڸ�Ѹ���800Ԫ��������4000Ԫ��Ӧ���ɳ���800Ԫ���Dz��ָ�ѵ�14%��˰��
�۸��Ϊ4000Ԫ�����4000Ԫ��Ӧ����ȫ����ѵ�11%��˰��
�Ը���������˰�ļ��㷽������
��1��������ʦ��õĸ��Ϊ2400Ԫ����Ӧ��˰ Ԫ��������ʦ��õĸ��Ϊ4000Ԫ����Ӧ��˰ Ԫ��
��2��������ʦ���Ѻ���˰420Ԫ������ʸ���Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У��Խ���AC��6��BD��8��M��N�ֱ���BC��CD�ϵĶ��㣬P���߶�BD�ϵ�һ�����㣬��PM��PN����Сֵ�ǣ� ��

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=![]() x2+1����ͼ��ʾ����
x2+1����ͼ��ʾ����
��1����գ������ߵĶ��������������������������Գ������� ����
��2����ͼ1����֪y����һ��A��0��2������P���������ϣ�����P��PB��x�ᣬ����ΪB������PAB�ǵȱ������Σ����P�����ꣻ
��3����ͼ���ڵڶ��ʵĻ����ϣ�������������һ��C��x��y��������AC��OC��BC��PC������OAC�����������BCP�����ʱ����C�ĺ�������
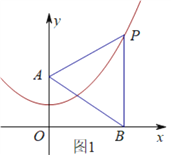
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com