
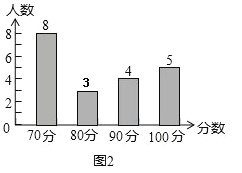
����Ŀ���ס�����У�μ���ѧ��������У�μӳ�����������ȣ�������������ѧ���ɼ��ֱ�Ϊ 70 �֡�80 �֡�90 �֡�100 �֣�����ͳ�����ݻ����������в�������ͳ��ͼ����
��У�ɼ�ͳ�Ʊ���
���� | 70 �� | 80 �� | 90 �� | 100 �� |
���� | 11 | 0 | 8 |

(1)��ͼ 1 �У���80 �������ڵ����ε�Բ�Ľǵ��� �ȣ�
(2)�뽫��У�ɼ�ͳ�Ʊ���ͼ 2 ����У�ɼ�����ͳ��ͼ����������
(3)������У��ƽ���ֺͼ�У����λ����
(4)����ؽ�����Ҫ��֯ 8 �˵Ĵ����Ӳμ��м�����������������Ϊ�˱��ڹ�����������������ѧУ�е�һ����ѡ����ѡ�֣�����ΪӦѡ�ĸ�ѧУ�����Ҫ˵�����ɣ�
���𰸡���1��54������2����������3����У��ƽ����Ϊ83�֣� ��У��λ��Ϊ70����4��ѡ��У�����ɼ�����
��������
��1����������ͳ��ͼ�������Բ�ĽǶ����������;
��2��������У�μӳ�����������������У90�ֵ����������ɲ�ȫ��У�ɼ�ͳ�Ʊ���У�ɼ�����ͳ��ͼ��
��3�����ݼ�Ȩƽ�����Ķ�������λ���Ķ��弴����⣻
��4���۲���У�ĸ߷��������з�������.
��1����80 �������ڵ����ε�Բ�Ľǵ���360��-90��-72��-144��=54����
��2��5��25%=20���ˣ�20��![]() =3���ˣ�
=3���ˣ�
��У90�ֵ�������20-11-8=1�ˣ�
��ȫ������ͳ��ͼ���£�
���� | 70 �� | 80 �� | 90 �� | 100 �� |
���� | 11 | 0 | 1 | 8 |
��3����У��ƽ����Ϊ��70��8+80��3+90��4+100��5����20=83��
��У��10,11���ķ���Ϊ70,70������λ��Ϊ70��
��4����У100�ֵ�����Ϊ8�ˣ���У100�ֵ�����Ϊ5�ˣ�
��ѡ��У.


 �ľ�ͼ���ʱ�ȷ�ϵ�д�
�ľ�ͼ���ʱ�ȷ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ϣ���OΪԭ�㣬��A��Ӧ����Ϊ9����B��Ӧ����Ϊb����C�ڵ�B�Ҳ࣬����Ϊ2����λ���߶�BC���������ƶ���
![]()
��1����b��5ʱ�������߶�AC�ij���
��2�����߶�BC��������������AO�����ƶ��Ĺ����У�������AC��OB��![]() AB�����ʱ����������bֵ��
AB�����ʱ����������bֵ��
��3�����߶�BC���������ƶ�ʱ�������ϵʽ|AC��OB|��|AB��OC|�����ʱ��b��ȡֵ��Χ���� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ѧ��ȤС�����Ժ���y=x![]() 2|x|��ͼ������ʽ�����̽����̽���������£��벹��������
2|x|��ͼ������ʽ�����̽����̽���������£��벹��������
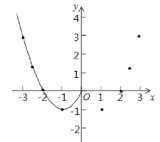
(1)�Ա���x��ȡֵ��Χ��ȫ��ʵ����x��y�ļ����Ӧֵ�б����£�
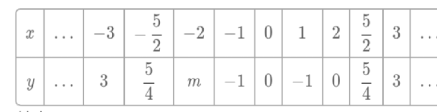
����m=___.
(2)���ݱ������ݣ�����ͼ��ʾ��ƽ��ֱ������ϵ����㣬�������˺���ͼ���һ���֣��뻭���ú���ͼ�����һ����.
(3)̽������ͼ���֣�
�ٺ���ͼ����x����___������,���Զ�Ӧ�ķ���x![]() 2|x|=0��___��ʵ������
2|x|=0��___��ʵ������
�ڷ���x![]() 2|x|=
2|x|=![]() ��___��ʵ������
��___��ʵ������
�۹���x�ķ���x![]() 2|x|=a��4��ʵ����ʱ��a��ȡֵ��Χ��___.
2|x|=a��4��ʵ����ʱ��a��ȡֵ��Χ��___.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
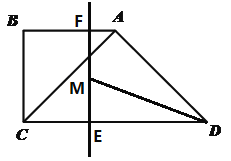
����Ŀ����ͼ��������ֽƬABCD�У�AB��2����A��60����������ֽƬ���ۣ�ʹ��A����CD���е�E�����ۺ�ΪFG����F��G�ֱ��ڱ�AB��AD�ϣ���cos��EFG��ֵΪ________��
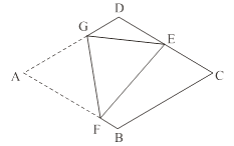
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ӳ��������һ������ɱ�Ϊ18Ԫ���͵��ӳ�Ʒ��Ͷ���г������������������飬�õ�ÿ��������y������������۵���x��Ԫ��֮��IJ����������£�
���۵���x��Ԫ/���� | �� | 20 | 25 | 30 | 35 | �� |
ÿ��������y������� | �� | 60 | 50 | 40 | 30 | �� |
��1�����ÿ��������y������������۵���x��Ԫ��֮��ĺ�����ϵʽ��
��2�����ÿ�µ�����z����Ԫ�������۵�x��Ԫ��֮��ĺ�����ϵʽ��
��3��������ز��Ź涨�����ֵ��Ӳ�Ʒ�����������ʲ��ܸ���50%�����Ҹõ��ӳ���������ֲ�Ʒÿ�µ�����ɱ����ܳ���900��Ԫ����ô����������۵��۶�Ϊ����Ԫʱ������ÿ���ܻ�����������������Ƕ��٣�������=�ۼ۩�����ɱ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
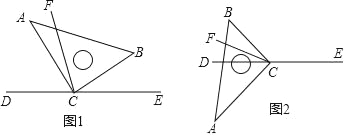
����Ŀ��ֱ�����ǰ�ABC��ֱ�Ƕ���C��ֱ��DE�ϣ�CFƽ�֡�BCD��
��1����ͼ1�У�����BCE=40�������ACF�Ķ�����
��2����ͼ1�У�����BCE=����ֱ��д����ACF�Ķ������ú�����ʽ�ӱ�ʾ����
��3����ͼ1�е����ǰ�ABC�ƶ���C��ת��ͼ2��λ�ã�̽����д����ACF���BCE�Ķ���֮��Ĺ�ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��P��Q��B��һ���������������ϣ���A��ʾ��-3����B��ʾ��3��������P�ӵ�A������ÿ��1����λ�������յ�B�����˶���ͬʱ����Q�ӵ�B������ÿ��2����λ�������յ�A�����˶�������һ�㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶�����BP=3AQʱ����P�������ϱ�ʾ������( )

A.2.4B.-1.8C.0.6D.-0.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�Ķ���D��DE��AC��BC���ӳ����ڵ�E��
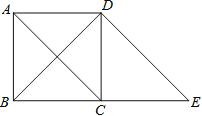
��1���ж��ı���ACED����״����˵�����ɣ�
��2����BD=8cm�����߶�BE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ֱ����������ͼ���ã���B=��CAD=90�㣬AB=BC=![]() cm��AC=AD����ֱ��CD��ֱ��a�ӵ�C��������ÿ��
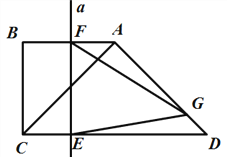
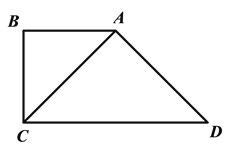
cm��AC=AD����ֱ��CD��ֱ��a�ӵ�C��������ÿ��![]() cm���ٶ���CD��������ƽ�ƣ���CD���ڵ�E��������BAD���ڵ�F�����ͬʱ����G�ӵ�D��������ÿ��1cm���ٶ�����DA�ķ����˶�������G����ֱ��a�ϣ���G��ֱ��aͬʱֹͣ�˶������˶�ʱ��Ϊt�루t>0��.
cm���ٶ���CD��������ƽ�ƣ���CD���ڵ�E��������BAD���ڵ�F�����ͬʱ����G�ӵ�D��������ÿ��1cm���ٶ�����DA�ķ����˶�������G����ֱ��a�ϣ���G��ֱ��aͬʱֹͣ�˶������˶�ʱ��Ϊt�루t>0��.
��1����գ�CD=_______cm;
��2������EG��FG�����EFG�����Ϊy����y��t֮��ĺ�����ϵʽ����д����Ӧt��ȡֵ��Χ��
��3���Ƿ����ijһʱ��t��0<t<2��,����ADC��ƽ����DM��EF�ڵ�M���Ƿ���ڵ�M��EF���е㣿�����ڣ����ʱ��tֵ���������ڣ���˵�����ɡ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com