
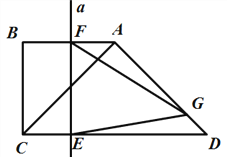
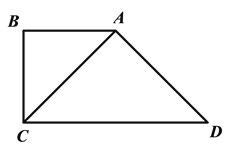
【题目】两个等腰直角三角形如图放置,∠B=∠CAD=90°,AB=BC=![]() cm,AC=AD,垂直于CD的直线a从点C出发,以每秒
cm,AC=AD,垂直于CD的直线a从点C出发,以每秒![]() cm的速度沿CD方向匀速平移,与CD交于点E,与折线BAD交于点F;与此同时,点G从点D出发,以每秒1cm的速度沿着DA的方向运动;当点G落在直线a上,点G与直线a同时停止运动;设运动时间为t秒(t>0).
cm的速度沿CD方向匀速平移,与CD交于点E,与折线BAD交于点F;与此同时,点G从点D出发,以每秒1cm的速度沿着DA的方向运动;当点G落在直线a上,点G与直线a同时停止运动;设运动时间为t秒(t>0).
(1)填空:CD=_______cm;
(2)连接EG、FG,设△EFG的面积为y,求y与t之间的函数关系式,并写出相应t的取值范围;
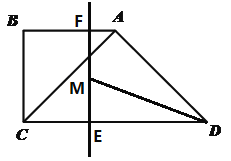
(3)是否存在某一时刻t(0<t<2),作∠ADC的平分线DM交EF于点M,是否存在点M是EF的中点?若存在,求此时的t值;若不存在,请说明理由。
【答案】(1)4![]() ;(2)①当
;(2)①当![]() 时,
时,![]() ;②当
;②当![]() 时,
时,![]() ;(3)3-
;(3)3-![]() .
.
【解析】分析:
(1)由∠B=∠CAD=90°,AB=BC=![]() cm,可得AC=4,结合AC=AD可得CD=
cm,可得AC=4,结合AC=AD可得CD=![]() ;
;
(2)由题意可知,当直线a过点A时,t=2,当直线a过点G时,t=![]() ;因此需分0<t≤2和2<t<
;因此需分0<t≤2和2<t<![]() (当t=
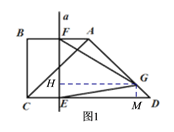
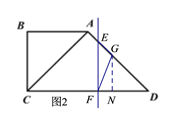
(当t=![]() 时,运动停止了)两段分别进行讨论,画出对应的图形如下图1和图2,作出如图所示的辅助线,结合已知条件分析、计算即可得到对应的y与t的函数关系式;
时,运动停止了)两段分别进行讨论,画出对应的图形如下图1和图2,作出如图所示的辅助线,结合已知条件分析、计算即可得到对应的y与t的函数关系式;
(3)如图3,当DM平分∠ADC时,延长DM交AB的延长线于点Q,过点D作DN⊥AB,并交BA的延长线于点N,由已知条件易得AQ=AD,AN=DN,由此即可求得QN的长,结合EM=![]() EF=
EF=![]() DN、EF∥DN可得DF=EN=
DN、EF∥DN可得DF=EN=![]() ,再由CF=CD-DF即可求得CF的长,由此即可求得对应的t的值.
,再由CF=CD-DF即可求得CF的长,由此即可求得对应的t的值.
详解:
(1)∵在△ABC中,AB=CB=![]() ,∠ABC=90°,
,∠ABC=90°,
∴AC=![]() ,
,
又∵在△ACD中,AC=AD,∠CAD=90°,
∴CD=![]() ;
;
(2)由题意可得,当t=2时,直线a过点A;点G在水平方向上的移动速度为![]() cm/秒,由此可得当t=
cm/秒,由此可得当t=![]() 时,直线a过点G;由此可分以下两种情况讨论y与t间的函数关系:
时,直线a过点G;由此可分以下两种情况讨论y与t间的函数关系:
①如图1,当![]() 时,过点G作GM⊥CD于点M,GH⊥EF于点H,由题意可得EF=BC=
时,过点G作GM⊥CD于点M,GH⊥EF于点H,由题意可得EF=BC=![]() ,CE=
,CE=![]() ,MD=
,MD=![]() GD=
GD=![]() ,GH=ME,
,GH=ME,
∴GH=CD-CE-MD=![]() ,
,
∴y=S△EFG=![]() EF·GH=
EF·GH=![]() (
(![]() ),
),
即:当![]() 时,
时,![]() ;
;
②如图2,当![]() 时,过点G作GN⊥CD于点N,由题意可得EF=DF=CD-CF=
时,过点G作GN⊥CD于点N,由题意可得EF=DF=CD-CF=![]() ,GN=DN=
,GN=DN=![]() DG=
DG=![]() ,
,
∴FN=CD-CF-DN=![]() ,
,
∴y=S△EFG=![]() EF·FN=
EF·FN=![]() ,
,
化简整理得:当![]() 时,
时,![]() ;
;
综上所述,y与t间的函数关系式为:①当![]() 时,
时,![]() ;②当
;②当![]() 时,
时,![]() ;
;
(3)存在符合要求的点M,如图3,当DM平分∠ADC时,延长DM交AB的延长线于点Q,过点D作DN⊥AB,并交BA的延长线于点N,
∵∠B=∠CAD=90°,AB=BC,AC=AD,
∴∠ACB=∠ACD=∠ADC=45°,
∴∠BCD=90°,
∴∠ABC+∠BCD=180°,
∴AB∥CD,
∴∠Q=∠CDQ,∠DAN=∠ADC=45°,
∵DM平分∠ADC,DN⊥AB于点N,
∴∠ADQ=∠CDQ=∠Q,∠DAN=∠ADN=45°,
∴AQ=AD=4,AN=DN=![]() AD=
AD=![]() ,
,
∴QN=AQ+AN=![]() ,
,
由题意可知EF⊥AB,又∵AB∥CD,DN⊥AB,
∴可得四边形EFDN是矩形,
∴EF=DN,EN=DF,
∵M为EF的中点,
∴EM=![]() EF =
EF =![]() DN,
DN,
∵DF∥DN,
∴△QEM∽△QNB,
∴QE:QN=EM:DN=1:2,
∴QE=![]() QN=
QN=![]() ,
,
∴DF=EN=QN-QE=![]() ,
,
∴CF=CD-DF=![]() ,
,
∴![]() .
.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两校参加数学竞赛,两校参加初赛的人数相等.初赛结束后,发现学生成绩分别为 70 分、80 分、90 分、100 分.依据统计数据绘制了如下尚不完整的统计图表.
甲校成绩统计表:
分数 | 70 分 | 80 分 | 90 分 | 100 分 |
人数 | 11 | 0 | 8 |

(1)在图 1 中,“80 分”所在的扇形的圆心角等于 度;
(2)请将甲校成绩统计表和图 2 的乙校成绩条形统计图补充完整;
(3)计算乙校的平均分和甲校的中位数;
(4)如果县教育局要组织 8 人的代表队参加市级复赛(团体赛),为了便于管理,决定从这两所学校中的一所挑选参赛选手,你认为应选哪个学校?请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
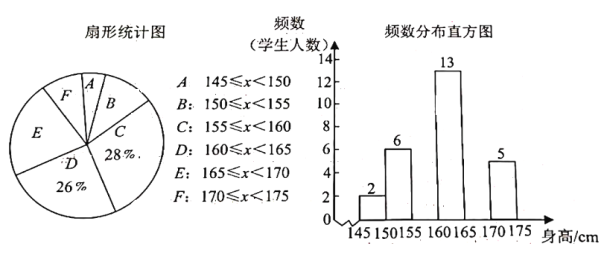
【题目】体育老师统计了七年级甲、乙两个班女生的身高情况,并绘制了如下不完整的统计图.请根据图中信息,解决下列问题:
(1)求甲、乙两个班共有女生多少人?
(2)请将频数分布直方图补充完整;
(3)求扇形统计图中![]() 部分所对应的扇形圆心角的度数.
部分所对应的扇形圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到 △A1BC1.
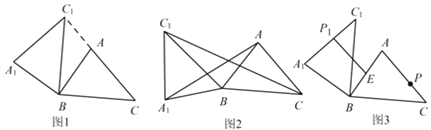
(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;
(2)如图2,连接AA1,CC1.若△ABA1的面积为4,求△CBC1的面积;
(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC 绕点 B 按逆时针方向旋转过程中,点P的对应点是点P1,求线段EP1长度的最大值与最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
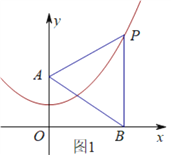
【题目】已知抛物线y=![]() x2+1(如图所示).
x2+1(如图所示).
(1)填空:抛物线的顶点坐标是( , ),对称轴是 ;
(2)如图1,已知y轴上一点A(0,2),点P在抛物线上,过点P作PB⊥x轴,垂足为B.若△PAB是等边三角形,求点P的坐标;
(3)如图,在第二问的基础上,在抛物线上有一点C(x,y),连接AC、OC、BC、PC,当△OAC的面积等于△BCP的面积时,求C的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四个函数:①y=﹣![]() ;②y=2(x+1)2﹣3;③y=﹣2x+5;④y=3x﹣10.其中,当x>﹣1时,y随x的增大而增大的函数是( )
;②y=2(x+1)2﹣3;③y=﹣2x+5;④y=3x﹣10.其中,当x>﹣1时,y随x的增大而增大的函数是( )
A. ①④ B. ②③ C. ②④ D. ①②
查看答案和解析>>
科目:初中数学 来源: 题型:
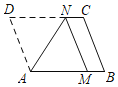
【题目】如图,将平行四边形ABCD折叠,使顶点D恰好落在AB边上的点M处,折痕为AN,有以下四个结论①MN∥BC;②MN=AM;③四边形MNCB是矩形;④四边形MADN是菱形,以上结论中,你认为正确的有_____________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
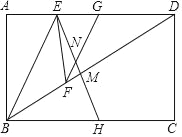
【题目】如图,在矩形ABCD中,EH垂直平分BD,交BD于点M,过BD上一点F作FG∥BE,FG恰好平分∠EFD,FG与EH交于点N.
(1)求证:DEDG=DFBF;
(2)若AB=3,AD=9,求FN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com