
ЁОЬтФПЁПдкШёНЧЁїABCжаЃЌAB=4ЃЌBC=5ЃЌЁЯACB=45ЁуЃЌНЋЁїABCШЦЕуBАДФцЪБеыЗНЯђа§зЊЃЌЕУЕН ЁїA1BC1ЃЎ
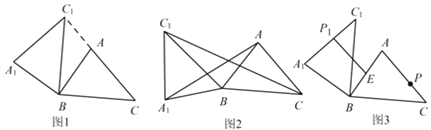
ЃЈ1ЃЉШчЭМ1ЃЌЕБЕуC1дкЯпЖЮCAЕФбгГЄЯпЩЯЪБЃЌЧѓЁЯCC1A1ЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌСЌНгAA1ЃЌCC1ЃЎШєЁїABA1ЕФУцЛ§ЮЊ4ЃЌЧѓЁїCBC1ЕФУцЛ§ЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌЕуEЮЊЯпЖЮABжаЕуЃЌЕуPЪЧЯпЖЮACЩЯЕФЖЏЕуЃЌдкЁїABC ШЦЕу B АДФцЪБеыЗНЯђа§зЊЙ§ГЬжаЃЌЕуPЕФЖдгІЕуЪЧЕуP1ЃЌЧѓЯпЖЮEP1ГЄЖШЕФзюДѓжЕгызюаЁжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ90ЁуЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() ЃЌ7.
ЃЌ7.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉгЩа§зЊЕФаджЪПЩЕУЃКЁЯA1C1B=ЁЯACB=45ЁуЃЌBC=BC1ЃЌИљОнЕШБпЖдЕШНЧЕУЕНЁЯCC1B=ЁЯC1CB=45ЁуЃЌИљОнЁЯCC1A1=ЁЯCC1B+ЁЯA1C1BЕУНтЃЛ
ЃЈ2ЃЉЭЈЙ§жЄУїЁїABA1ЁзЁїCBC1ЃЌРћгУЯрЫЦШ§НЧаЮЕФУцЛ§БШЕШгкЯрЫЦБШЕФЦНЗНЕУЕНЃЌ ЃЌОнДЫНтЕУЁїCBC1ЕФУцЛ§ЃЛ
ЃЌОнДЫНтЕУЁїCBC1ЕФУцЛ§ЃЛ
ЃЈ3ЃЉЙ§ЕуBзїBDЁЭACЃЌDЮЊДЙзуЃЌЧѓЕУBD=![]() ЃЌЂйЕБPдкACЩЯдЫЖЏжСДЙзуЕуDЃЌЪЙЕуPЕФЖдгІЕуP1дкЯпЖЮABЩЯЪБЃЌEP1=BP1ЉBEЃЛЂкЕБPдкACЩЯдЫЖЏжСЕуCЃЌЪЙЕуPЕФЖдгІЕуP1дкЯпЖЮABЕФбгГЄЯпЩЯЪБЃЌEP1зюДѓЃЌEP1=BC+BEЃЎ
ЃЌЂйЕБPдкACЩЯдЫЖЏжСДЙзуЕуDЃЌЪЙЕуPЕФЖдгІЕуP1дкЯпЖЮABЩЯЪБЃЌEP1=BP1ЉBEЃЛЂкЕБPдкACЩЯдЫЖЏжСЕуCЃЌЪЙЕуPЕФЖдгІЕуP1дкЯпЖЮABЕФбгГЄЯпЩЯЪБЃЌEP1зюДѓЃЌEP1=BC+BEЃЎ
ЪдЬтНтЮіЃКНтЃКЃЈ1ЃЉЁпгЩа§зЊЕФаджЪПЩЕУЃКЁЯA1C1B=ЁЯACB=45ЁуЃЌBC=BC1ЃЌ
ЁрЁЯCC1B=ЁЯC1CB=45ЁуЃЌ
ЁрЁЯCC1A1=ЁЯCC1B+ЁЯA1C1B=45Ёу+45Ёу=90ЁуЃЛ
ЃЈ2ЃЉЁпгЩа§зЊЕФаджЪПЩЕУЃКЁїABCЁеЁїA1BC1ЃЌ
ЁрBA=BA1ЃЌBC=BC1ЃЌЁЯABC=ЁЯA1BC1ЃЌ
Ёр![]() ЃЌЁЯABC+ЁЯABC1=ЁЯA1BC1+ЁЯABC1ЃЌ
ЃЌЁЯABC+ЁЯABC1=ЁЯA1BC1+ЁЯABC1ЃЌ
ЁрЁЯABA1=ЁЯCBC1ЃЌ
ЁрЁїABA1ЁзЁїCBC1ЃЌ
Ёр ЃЌ
ЃЌ
ЁпSЁїABA1=4ЃЌЁрSЁїCBC1=![]() ЃЎ
ЃЎ
ЃЈ3ЃЉЙ§ЕуBзїBDЁЭACЃЌDЮЊДЙзуЃЌ
ЁпЁїABCЮЊШёНЧШ§НЧаЮЃЌЁрЕуDдкЯпЖЮACЩЯЃЌ
дкRtЁїBCDжаЃЌBD=BCЁСsin45Ёу=![]() ЃЌ
ЃЌ
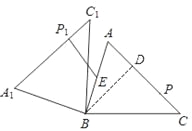
ЂйШчЭМ1ЃЌЕБPдкACЩЯдЫЖЏжСДЙзуЕуDЃЌЁїABCШЦЕуBа§зЊЃЌЪЙЕуPЕФЖдгІЕуP1дкЯпЖЮABЩЯЪБЃЌEP1зюаЁЃЎзюаЁжЕЮЊЃКEP1=BP1ЉBE=BDЉBE=![]() Љ2ЃЎ
Љ2ЃЎ
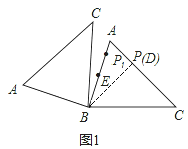
ЂкШчЭМ2ЃЌЕБPдкACЩЯдЫЖЏжСЕуCЃЌЁїABCШЦЕуBа§зЊЃЌЪЙЕуPЕФЖдгІЕуP1дкЯпЖЮABЕФбгГЄЯпЩЯЪБЃЌEP1зюДѓЃЌзюДѓжЕЮЊЃКEP1=BC+BE=5+2=7ЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
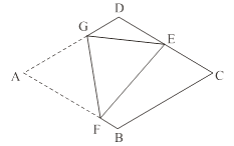
ЁОЬтФПЁПШчЭМЃЌдкСтаЮжНЦЌABCDжаЃЌABЃН2ЃЌЁЯAЃН60ЁуЃЌНЋСтаЮжНЦЌЗелЃЌЪЙЕуAТфдкCDЕФжаЕуEДІЃЌелКлЮЊFGЃЌЕуFЁЂGЗжБ№дкБпABЁЂADЩЯЃЎдђcosЁЯEFGЕФжЕЮЊ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЙ§е§ЗНаЮABCDЕФЖЅЕуDзїDEЁЮACНЛBCЕФбгГЄЯпгкЕуEЃЎ
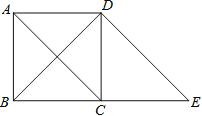
ЃЈ1ЃЉХаЖЯЫФБпаЮACEDЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШєBD=8cmЃЌЧѓЯпЖЮBEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
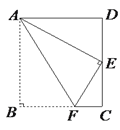
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDЮЊОиаЮжНЦЌЃЌАбжНЦЌABCDелЕўЃЌЪЙЕуBЧЁКУТфдкCDБпЕФжаЕуEДІ, елКлЮЊAFЃЌШєCD=6ЃЌдђAFЕШгк__________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
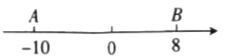
ЁОЬтФПЁПФГЙЋЫОЯњЪлвЛжжНјМлЮЊ20дЊ/ИіЕФМЦЫуЦїЃЌЦфЯњЪлСПyЃЈЭђИіЃЉгыЯњЪлМлИёxЃЈдЊ/ИіЃЉ ЕФБфЛЏШчЯТБэЃКЭЌЪБЃЌЯњЪлЙ§ГЬжаЕФЦфЫћПЊжЇЃЈВЛКЌНјМлЃЉзмМЦ40ЭђдЊЃЎ
ЯњЪлМлИёx(дЊ/Иі) | Ё | 30 | 40 | 50 | 60 | Ё |
ЯњЪлСПy(ЭђИі) | Ё | 5 | 4 | 3 | 2 | Ё |
ЃЈ1ЃЉЙлВьВЂЗжЮіБэжаЕФЪ§ОнЃЌгУЫљбЇЙ§ЕФКЏЪ§жЊЪЖЃЌжБНгаДГіyгы xЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉЧѓГіИУЙЋЫОЯњЪлетжжМЦЫуЦїЕФОЛЕУРћШѓzЃЈЭђдЊЃЉгыЯњЪлМлИё xЃЈдЊ/ИіЃЉ ЕФКЏЪ§НтЮіЪНЃЌЯњЪлМлИёЖЈЮЊЖрЩйдЊЪБОЛЕУРћШѓзюДѓЃЌзюДѓжЕЪЧЖрЩй?
ЃЈ3ЃЉИУЙЋЫОвЊЧѓОЛЕУРћШѓВЛФмЕЭгк40ЭђдЊЃЌЧыФуНсКЯКЏЪ§ЭМЯѓЧѓГіЯњЪлМлИё xЃЈдЊ/ИіЃЉ ЕФШЁжЕЗЖЮЇЃЌШєЛЙашПМТЧЯњЪлСПОЁПЩФмДѓЃЌЯњЪлМлИёгІЖЈЮЊЖрЩйдЊ ?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЪ§жсЪЧбЇЯАГѕжаЪ§бЇЕФ- -ИіживЊЙЄОпРћгУЪ§жсПЩвдНЋЪ§гыаЮЭъУРЕиНсКЯЃЎбаОПЪ§жсЮвУЧЗЂЯжСЫаэЖрживЊЕФЙцТЩЃКЪ§жсЩЯЕу![]() ЁЂЕу
ЁЂЕу![]() БэЪОЕФЪ§ЮЊ
БэЪОЕФЪ§ЮЊ![]() ЃЌдђ
ЃЌдђ![]() СНЕужЎМфЕФОрРы
СНЕужЎМфЕФОрРы![]() ЃЌШє
ЃЌШє![]() ЃЌдђПЩМђЛЏЮЊЃЛ
ЃЌдђПЩМђЛЏЮЊЃЛ![]() ЯпЖЮ
ЯпЖЮ![]() ЕФжаЕу
ЕФжаЕу![]() БэЪОЕФЪ§ЮЊ
БэЪОЕФЪ§ЮЊ![]() ШчЭМЃЌвбжЊЪ§жсЩЯга
ШчЭМЃЌвбжЊЪ§жсЩЯга![]() СНЕуЃЌЗжБ№БэЪОЕФЪ§ЮЊ
СНЕуЃЌЗжБ№БэЪОЕФЪ§ЮЊ![]() ЃЌЕу
ЃЌЕу![]() вдУПУы
вдУПУы![]() ИіЕЅЮЛГЄЖШЕФЫйЖШбиЪ§жсЯђгвдШЫйдЫЖЏЃЌЕу
ИіЕЅЮЛГЄЖШЕФЫйЖШбиЪ§жсЯђгвдШЫйдЫЖЏЃЌЕу![]() вдУПУы
вдУПУы![]() ИіЕЅЮЛГЄЖШЯђзѓдШЫйдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊ
ИіЕЅЮЛГЄЖШЯђзѓдШЫйдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊ![]() Уы
Уы![]() ЃЎ
ЃЎ
ЃЈ1ЃЉдЫЖЏПЊЪМЧАЃЌ![]() СНЕуЕФОрРыЮЊЖрЩйИіЕЅЮЛГЄЖШЃЛЯпЖЮ
СНЕуЕФОрРыЮЊЖрЩйИіЕЅЮЛГЄЖШЃЛЯпЖЮ![]() ЕФжаЕу
ЕФжаЕу![]() ЫљБэЪОЕФЪ§ЮЊЃП
ЫљБэЪОЕФЪ§ЮЊЃП
ЃЈ2ЃЉЕу![]() дЫЖЏ
дЫЖЏ![]() УыКѓЫљдкЮЛжУЕФЕуБэЪОЕФЪ§ЮЊ ЃЛЕу
УыКѓЫљдкЮЛжУЕФЕуБэЪОЕФЪ§ЮЊ ЃЛЕу ![]() дЫЖЏ
дЫЖЏ![]() УыКѓЫљдкЮЛжУЕФЕуБэЪОЕФЪ§ЮЊ ЃЎ (гУКЌ
УыКѓЫљдкЮЛжУЕФЕуБэЪОЕФЪ§ЮЊ ЃЎ (гУКЌ![]() ЕФЪНзгБэЪО
ЕФЪНзгБэЪО
ЃЈ3ЃЉЫќУЧАДЩЯЪіЗНЪНдЫЖЏЃЌ![]() СНЕуОЙ§ЖрЩйУыЛсЯрОр
СНЕуОЙ§ЖрЩйУыЛсЯрОр![]() ИіЕЅЮЛГЄЖШ?
ИіЕЅЮЛГЄЖШ?
ЃЈ4ЃЉШє![]() АДЩЯЪіЗНЪНдЫЖЏЃЌ
АДЩЯЪіЗНЪНдЫЖЏЃЌ ![]() СНЕуОЙ§ЖрЩйУыЃЌЯпЖЮ
СНЕуОЙ§ЖрЩйУыЃЌЯпЖЮ![]() ЕФжаЕу
ЕФжаЕу![]() гыдЕужиКЯ?
гыдЕужиКЯ?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПСНИіЕШбќжБНЧШ§НЧаЮШчЭМЗХжУЃЌЁЯB=ЁЯCAD=90ЁуЃЌAB=BC=![]() cmЃЌAC=ADЃЌДЙжБгкCDЕФжБЯпaДгЕуCГіЗЂЃЌвдУПУы
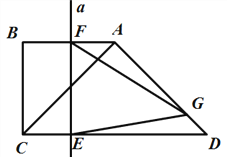
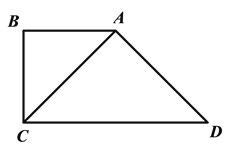
cmЃЌAC=ADЃЌДЙжБгкCDЕФжБЯпaДгЕуCГіЗЂЃЌвдУПУы![]() cmЕФЫйЖШбиCDЗНЯђдШЫйЦНвЦЃЌгыCDНЛгкЕуEЃЌгыелЯпBADНЛгкЕуFЃЛгыДЫЭЌЪБЃЌЕуGДгЕуDГіЗЂЃЌвдУПУы1cmЕФЫйЖШбизХDAЕФЗНЯђдЫЖЏЃЛЕБЕуGТфдкжБЯпaЩЯЃЌЕуGгыжБЯпaЭЌЪБЭЃжЙдЫЖЏЃЛЩшдЫЖЏЪБМфЮЊtУыЃЈt>0ЃЉ.
cmЕФЫйЖШбиCDЗНЯђдШЫйЦНвЦЃЌгыCDНЛгкЕуEЃЌгыелЯпBADНЛгкЕуFЃЛгыДЫЭЌЪБЃЌЕуGДгЕуDГіЗЂЃЌвдУПУы1cmЕФЫйЖШбизХDAЕФЗНЯђдЫЖЏЃЛЕБЕуGТфдкжБЯпaЩЯЃЌЕуGгыжБЯпaЭЌЪБЭЃжЙдЫЖЏЃЛЩшдЫЖЏЪБМфЮЊtУыЃЈt>0ЃЉ.
ЃЈ1ЃЉЬюПеЃКCD=_______cm;
ЃЈ2ЃЉСЌНгEGЁЂFGЃЌЩшЁїEFGЕФУцЛ§ЮЊyЃЌЧѓyгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіЯргІtЕФШЁжЕЗЖЮЇЃЛ
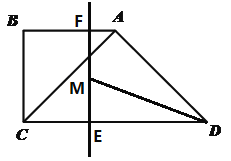
ЃЈ3ЃЉЪЧЗёДцдкФГвЛЪБПЬtЃЈ0<t<2ЃЉ,зїЁЯADCЕФЦНЗжЯпDMНЛEFгкЕуMЃЌЪЧЗёДцдкЕуMЪЧEFЕФжаЕуЃПШєДцдкЃЌЧѓДЫЪБЕФtжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯBAC=90ЁуЃЌADЪЧжаЯпЃЌEЪЧADЕФжаЕуЃЌЙ§ЕуAзїAFЁЮBCНЛBEЕФбгГЄЯпгкFЃЌСЌНгCFЃЌЧѓжЄЃКЫФБпаЮADCFЪЧСтаЮЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDЪЧБпГЄЮЊ6ЕФе§ЗНаЮЃЌЕуEдкБпABЩЯЃЌBEЃН4ЃЌЙ§ЕуEзїEFЁЮBCЃЌЗжБ№НЛBDЁЂCDгкGЁЂFСНЕуЃЎШєMЁЂNЗжБ№ЪЧDGЁЂCEЕФжаЕуЃЌдђMNЕФГЄЮЊ ЃЈ ЃЉ

A. 3 B. ![]() C.
C. ![]() D. 4
D. 4
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com