
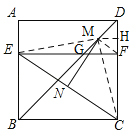
【题目】如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD、CD于G、F两点.若M、N分别是DG、CE的中点,则MN的长为 ( )

A. 3 B. ![]() C.
C. ![]() D. 4
D. 4
【答案】C
【解析】解:连接FM、EM、CM.∵四边形ABCD为正方形,∴∠ABC=∠BCD=∠ADC=90°,BC=CD.∵EF∥BC,∴∠GFD=∠BCD=90°,EF=BC,∴EF=BC=DC.∵∠BDC=![]() ∠ADC=45°,∴△GFD是等腰直角三角形.∵M是DG的中点,∴FM=DM=MG,FM⊥DG,∴∠GFM=∠CDM=45°,∴△EMF≌△CMD,∴EM=CM,过M作MH⊥CD于H,由勾股定理得:BD=
∠ADC=45°,∴△GFD是等腰直角三角形.∵M是DG的中点,∴FM=DM=MG,FM⊥DG,∴∠GFM=∠CDM=45°,∴△EMF≌△CMD,∴EM=CM,过M作MH⊥CD于H,由勾股定理得:BD=![]() =
=![]() ,EC=
,EC=![]() =
=![]() .∵∠EBG=45°,∴△EBG是等腰直角三角形,∴EG=BE=4,∴BG=
.∵∠EBG=45°,∴△EBG是等腰直角三角形,∴EG=BE=4,∴BG=![]() ,∴DM=
,∴DM=![]() ,∴MH=DH=1,∴CH=6﹣1=5,∴CM=EM=
,∴MH=DH=1,∴CH=6﹣1=5,∴CM=EM=![]() =
=![]() .∵CE2=EM2+CM2,∴∠EMC=90°.∵N是EC的中点,∴MN=
.∵CE2=EM2+CM2,∴∠EMC=90°.∵N是EC的中点,∴MN=![]() EC=
EC=![]() .故选C.
.故选C.


科目:初中数学 来源: 题型:
【题目】在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到 △A1BC1.
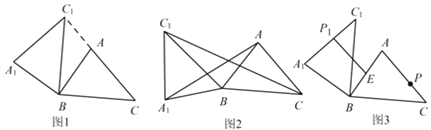
(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;
(2)如图2,连接AA1,CC1.若△ABA1的面积为4,求△CBC1的面积;
(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC 绕点 B 按逆时针方向旋转过程中,点P的对应点是点P1,求线段EP1长度的最大值与最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
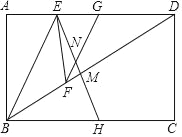
【题目】如图,在矩形ABCD中,EH垂直平分BD,交BD于点M,过BD上一点F作FG∥BE,FG恰好平分∠EFD,FG与EH交于点N.
(1)求证:DEDG=DFBF;
(2)若AB=3,AD=9,求FN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,点A,B,C表示的数分别是-6,10,12.点A以每秒3个单位长度的速度向右运动,同时线段BC以每秒1个单位长度的速度也向右运动.
(1)运动前线段AB的长度为________;
(2)当运动时间为多长时,点A和线段BC的中点重合?
(3)试探究是否存在运动到某一时刻,线段AB=![]() AC?若存在,求出所有符合条件的点A表示的数;若不存在,请说明理由.
AC?若存在,求出所有符合条件的点A表示的数;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学着说点理:补全证明过程:
如图,已知![]() ,
,![]() ,垂足分别为
,垂足分别为![]() ,
,![]() ,
,![]() ,试证明:
,试证明:![]() .请补充证明过程,并在括号内填上相应的理由.
.请补充证明过程,并在括号内填上相应的理由.
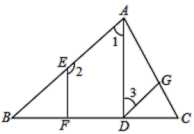
证明:∵![]() ,
,![]() (已知)
(已知)
∴![]() (___________________),
(___________________),
∴![]() (___________________),
(___________________),
∴________![]() (___________________).
(___________________).
又∵![]() (已知),
(已知),
∴![]() (___________________),
(___________________),
∴![]() ________(___________________),
________(___________________),
∴![]() (___________________).
(___________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某报社为了了解市民“获取新闻的最主要途径”,开展了一次抽样调查,根据调查结果绘制了如下三种不完整的统计图表.
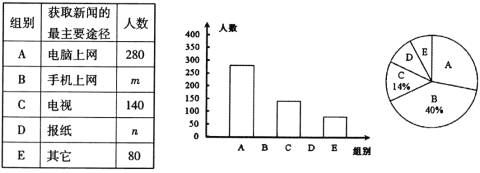
请根据图表信息解答下列问题:
(1)统计表中的![]() = ,
= ,![]() = ,并请补全条形统计图;
= ,并请补全条形统计图;
(2)扇形统计图中“![]() ”所对应的圆心角的度数是 ;
”所对应的圆心角的度数是 ;
(3)若该市约有100万人,请你估计其中将“电脑上网”和“手机上网”作为“获取新闻的最主要途径”的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与双曲线
与双曲线![]() 交于A、B两点,A点的横坐标为3,则下列结论:①k=3;②关于x的不等式
交于A、B两点,A点的横坐标为3,则下列结论:①k=3;②关于x的不等式![]() 的解集为
的解集为![]() 或
或![]() ;③若双曲线
;③若双曲线![]() 上有一点C的纵坐标为6,则△AOC的面积为8;④若在
上有一点C的纵坐标为6,则△AOC的面积为8;④若在![]() 轴上有一点M,
轴上有一点M,![]() 轴上有一点N,且点M、N、A、C四点恰好构成平行四边形,则M、N点的坐标分别为M(2,0)、N(0,4),其中正确结论的个数( )
轴上有一点N,且点M、N、A、C四点恰好构成平行四边形,则M、N点的坐标分别为M(2,0)、N(0,4),其中正确结论的个数( )
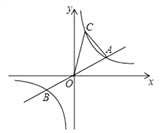
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车都从A地出发,在路程为360千米的同一道路上驶向B地.甲车先出发匀速驶向B地.10分钟后乙车出发,乙车匀速行驶3小时后在途中的配货站装货耗时20分钟.由于满载货物,乙车速度较之前减少了40千米/时.乙车在整个途中共耗时![]() 小时,结果与甲车同时到达B地.
小时,结果与甲车同时到达B地.
(1)甲车的速度为 千米/时;
(2)求乙车装货后行驶的速度;
(3)乙车出发 小时与甲车相距10千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com