
【题目】甲、乙两车都从A地出发,在路程为360千米的同一道路上驶向B地.甲车先出发匀速驶向B地.10分钟后乙车出发,乙车匀速行驶3小时后在途中的配货站装货耗时20分钟.由于满载货物,乙车速度较之前减少了40千米/时.乙车在整个途中共耗时![]() 小时,结果与甲车同时到达B地.
小时,结果与甲车同时到达B地.
(1)甲车的速度为 千米/时;
(2)求乙车装货后行驶的速度;
(3)乙车出发 小时与甲车相距10千米?
【答案】(1)80;(2)60千米/时;(3)![]() 或
或![]() 或
或![]() .
.
【解析】
(1)设甲车的速度为x千米/时,根据甲车时间比乙车时间多用10分钟,路程为360千米,列方程求解即可;
(2)设乙车装货后的速度为x千米/时,根据“满载货物后,乙车速度较之前减少了40千米/时.乙车在整个途中共耗时![]() 小时”列方程,求解即可;
小时”列方程,求解即可;
(3)分两种情况讨论:①装货前,设乙车出发x小时两车相距10千米,列方程求解即可;
②乙车装货后,设乙车又行驶了x小时与甲车相距10千米.列方程求出x的值,再加上3小时20分钟即可.
(1)设甲车的速度为x千米/时,根据题意得:
(![]() )x=360
)x=360
解得:x=80.
答:甲车的速度为80千米/时.
(2)设乙车装货后的速度为x千米/时,根据题意得:
![]()
解得:x=60.
答:乙车装货后行驶的速度为60千米/时.
(3)分两种情况讨论:
①装货前,设乙车出发x小时两车相距10千米,根据题意得:
![]()
解得:x=![]() 或x=
或x=![]() .
.
②乙车装货后,设乙车又行驶了x小时与甲车相距10千米.此时乙车在前,甲车在后.
乙车装货结束时,甲车行驶的路程=80×(3+![]() )=280(千米),乙车行驶的路程=100×3=300(千米).根据题意得:
)=280(千米),乙车行驶的路程=100×3=300(千米).根据题意得:
280+80x+10=300+60x
解得:x=0.5
乙车一共用了![]() (小时).
(小时).
答:乙车出发![]() 小时或
小时或![]() 小时或
小时或![]() 小时与甲车相距10千米.
小时与甲车相距10千米.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD、CD于G、F两点.若M、N分别是DG、CE的中点,则MN的长为 ( )

A. 3 B. ![]() C.
C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
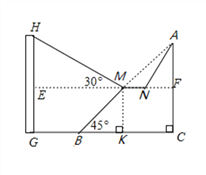
【题目】市政府对城市建设进行了整改,如图,已知斜坡AB长![]() 米,坡角(即∠ABC)为45°,AC⊥BC,现计划在斜坡中点M处挖去部分斜坡,修建一个平行于水平线CB的休闲平台MN和一条新的斜坡AN.(温馨提示:后两个小题结果都保留根号)
米,坡角(即∠ABC)为45°,AC⊥BC,现计划在斜坡中点M处挖去部分斜坡,修建一个平行于水平线CB的休闲平台MN和一条新的斜坡AN.(温馨提示:后两个小题结果都保留根号)
(1)若修建的斜坡AN的坡比为![]() ,求休闲平台MN的长是多少米?
,求休闲平台MN的长是多少米?
(2)一座建筑物GH距离B点34米远(BG=34米),小亮在M点测得建筑物顶部H的仰角(即∠HME)为30°.点A、C、B、G,H在同一个平面内,点C、B、G在同一条直线上,且HG⊥CG,问建筑物GH高为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
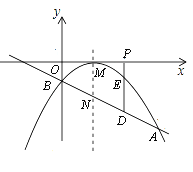
【题目】已知二次函数图象的顶点坐标为M(1,0),直线![]() 与该二次函数的图象交于A,B两点,其中A点的坐标为(3,-4),B点在y轴上.
与该二次函数的图象交于A,B两点,其中A点的坐标为(3,-4),B点在y轴上.
(1)求m的值及这个二次函数的解析式;
(2)在x轴上找一点Q,使△QAB的周长最小,并求出此时Q点坐标;
(3)若P(t,0)是x轴上的一个动点,过P作x轴的垂线分别与直线AB和二次函数的图象交于D、E两点.
①设线段DE的长为h,当0<t<3时,求h与t之间的函数关系式;
②若直线AB与抛物线的对称轴交点为N,问是否存在一点P,使以M、N、D、E为顶点的四边形是平行四边形?若存在,请求出此时P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 的顶点
的顶点![]() ,
,![]() ,点
,点![]() 在
在![]() 轴的正半轴上,按以下步骤作图:①以点
轴的正半轴上,按以下步骤作图:①以点![]() 为圆心、适当长度为半径作弧,分别交
为圆心、适当长度为半径作弧,分别交![]() 、
、![]() 于点
于点![]() ,
,![]() ;②分别以点
;②分别以点![]() ,
,![]() 为圆心、大于
为圆心、大于![]() 的长为半径作弧,两弧在
的长为半径作弧,两弧在![]() 内交于点
内交于点![]() ;③作射线
;③作射线![]() ,交边
,交边![]() 于点
于点![]() .则点
.则点![]() 的坐标为( )
的坐标为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD中,AB=4,点G是射线AB上的一个动点,以DG为边向右作正方形DGEF,作EH⊥AB于点H.
(1)若点G在点B的右边.试探索:EH![]() BG的值是否为定值,若是,请求出定值;若不是,请说明理由.
BG的值是否为定值,若是,请求出定值;若不是,请说明理由.

(2)连接EB,在G点的整个运动(点G与点A重合除外)过程中,求∠EBH的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() ,纵坐标
,纵坐标![]() 的对应值如下表:
的对应值如下表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
小聪观察上表,得出下面结论:①抛物线与x轴的一个交点为(3,0); ②函数![]() 的最大值为6;③抛物线的对称轴是
的最大值为6;③抛物线的对称轴是![]() ;④在对称轴左侧,y随x增大而增大.其中正确有( )
;④在对称轴左侧,y随x增大而增大.其中正确有( )
A. ①② B. ①③ C. ①②③ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在平面直角坐标系xOy中,点A(-4,0),点B在直线y=x+2上.当A、B两点间的距离最小时,点B的坐标是( )
A. (![]() ,
,![]() ) B. (
) B. (![]() ,
,![]() ) C. (-3,-1) D. (-3,
) C. (-3,-1) D. (-3,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种情况是等可能的,当三辆汽车经过这个十字路口时:
(1)求三辆车全部同向而行的概率;
(2)求至少有两辆车向左转的概率;
(3)由于十字路口右拐弯处是通往新建经济开发区的,因此交管部门在汽车行驶高峰时段对车流量作了统计,发现汽车在此十字路口向右转的频率为![]() ,向左转和直行的频率均为
,向左转和直行的频率均为![]() .目前在此路口,汽车左转、右转、直行的绿灯亮的时间分别为30秒,在绿灯亮总时间不变的条件下,为了缓解交通拥挤,请你用统计的知识对此路口三个方向的绿灯亮的时间做出合理的调整.
.目前在此路口,汽车左转、右转、直行的绿灯亮的时间分别为30秒,在绿灯亮总时间不变的条件下,为了缓解交通拥挤,请你用统计的知识对此路口三个方向的绿灯亮的时间做出合理的调整.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com