
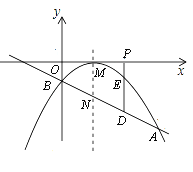
【题目】已知二次函数图象的顶点坐标为M(1,0),直线![]() 与该二次函数的图象交于A,B两点,其中A点的坐标为(3,-4),B点在y轴上.
与该二次函数的图象交于A,B两点,其中A点的坐标为(3,-4),B点在y轴上.
(1)求m的值及这个二次函数的解析式;
(2)在x轴上找一点Q,使△QAB的周长最小,并求出此时Q点坐标;
(3)若P(t,0)是x轴上的一个动点,过P作x轴的垂线分别与直线AB和二次函数的图象交于D、E两点.
①设线段DE的长为h,当0<t<3时,求h与t之间的函数关系式;
②若直线AB与抛物线的对称轴交点为N,问是否存在一点P,使以M、N、D、E为顶点的四边形是平行四边形?若存在,请求出此时P点的坐标;若不存在,请说明理由.
【答案】(1) ![]() ,m=-1;(2)
,m=-1;(2)![]() (
(![]() ,0);(3)①
,0);(3)①![]() ;
;
② 存在,理由见解析.
【解析】分析:(1)设抛物线的解析式为y=![]() ,将A点坐标分别代入抛物线和直线的解析式,即可求出抛物线的解析式和m的值;(2)使△QAB的周长最小,即是求AQ+BQ的值最小,作出B点关于x轴的对称点B′,当A、Q、B′三点在一条直线上时,△QAB的周长最小,求得直线AB'的解析式,即可求得点Q的坐标;(3)①根据P点坐标分别表示出D、E两点坐标,即可求出h与t之间的函数关系式;② 存在,分抛物线在直线上方时和抛物线在直线下方时两种情况求点P的坐标.
,将A点坐标分别代入抛物线和直线的解析式,即可求出抛物线的解析式和m的值;(2)使△QAB的周长最小,即是求AQ+BQ的值最小,作出B点关于x轴的对称点B′,当A、Q、B′三点在一条直线上时,△QAB的周长最小,求得直线AB'的解析式,即可求得点Q的坐标;(3)①根据P点坐标分别表示出D、E两点坐标,即可求出h与t之间的函数关系式;② 存在,分抛物线在直线上方时和抛物线在直线下方时两种情况求点P的坐标.
详解:
(1)∵二次函数图象的顶点M(1, 0), ∴二次函数可表达为y=![]()
又∵图象过A(3,-4),∴![]() =-4,解得a=-1,
=-4,解得a=-1,
∴二次函数解析式为: ![]() ,
,
A(3,- 4)在直线y = -x + m上:-3+m=-4,m=-1;
(2)由![]() 得B(0,-1),
得B(0,-1),
B关于x轴的对称点为B'(0, 1)
设直线AB'的解析式为:y=kx+1,将A(3,-4)代入得:-4=3k+1,解得k=-![]() ,
,
∴y=-![]() ,令y=0,得x=
,令y=0,得x=![]() ,
,
∴![]() (
(![]() ,0),此时A、Q、
,0),此时A、Q、![]() 在一条直线上,所以
在一条直线上,所以![]() ,
,
即△QAB的周长最小,![]() (
(![]() ,0),
,0),
(3)直线AB的解析式为:y=-x-1,抛物线为: ![]() ,
,
①∵0<t<3,∴h=-t+2t-1-(-t-1)=-t+3t ;
② 存在
∵ M(1,0)∴N(1,-2),∴MN=2, MN//DE,∴只要DE=MN=2即可
1)当抛物线在直线上方时,由-t+3t =2,解得t=1或t=2,
当t=1时MN与
2)当抛物线在直线下方时,由t+3t =2,解得![]() ,
,
此时![]() 和
和![]() ,综上所述P点共有:
,综上所述P点共有:
![]() ,
,![]() ,
,![]() 共三个
共三个


科目:初中数学 来源: 题型:
【题目】在数轴上,点A,B,C表示的数分别是-6,10,12.点A以每秒3个单位长度的速度向右运动,同时线段BC以每秒1个单位长度的速度也向右运动.
(1)运动前线段AB的长度为________;
(2)当运动时间为多长时,点A和线段BC的中点重合?
(3)试探究是否存在运动到某一时刻,线段AB=![]() AC?若存在,求出所有符合条件的点A表示的数;若不存在,请说明理由.
AC?若存在,求出所有符合条件的点A表示的数;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与双曲线
与双曲线![]() 交于A、B两点,A点的横坐标为3,则下列结论:①k=3;②关于x的不等式
交于A、B两点,A点的横坐标为3,则下列结论:①k=3;②关于x的不等式![]() 的解集为
的解集为![]() 或
或![]() ;③若双曲线
;③若双曲线![]() 上有一点C的纵坐标为6,则△AOC的面积为8;④若在
上有一点C的纵坐标为6,则△AOC的面积为8;④若在![]() 轴上有一点M,
轴上有一点M,![]() 轴上有一点N,且点M、N、A、C四点恰好构成平行四边形,则M、N点的坐标分别为M(2,0)、N(0,4),其中正确结论的个数( )
轴上有一点N,且点M、N、A、C四点恰好构成平行四边形,则M、N点的坐标分别为M(2,0)、N(0,4),其中正确结论的个数( )
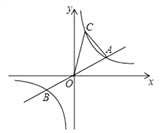
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前节能灯在城市已基本普及,某商场计划购进甲、乙两种节能订共1200只,这两种节能灯的进价、售价如下表:
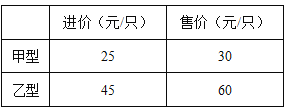
(1)如何进货,进货款恰好为46000元?
(2)为确保乙型节能灯顺利畅销,在(1)的条件下,商家决定对乙型节能灯进行打折出售,且全部售完后,乙型节能灯的利润率为20%,请同乙型节能灯需打几折?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,下列结论中,一定正确的个数是( )
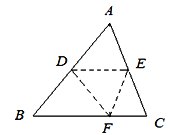
①△BDF是等腰三角形;
②DE=![]() BC;
BC;
③四边形ADFE是菱形;
④∠BDF+∠FEC=2∠A.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车都从A地出发,在路程为360千米的同一道路上驶向B地.甲车先出发匀速驶向B地.10分钟后乙车出发,乙车匀速行驶3小时后在途中的配货站装货耗时20分钟.由于满载货物,乙车速度较之前减少了40千米/时.乙车在整个途中共耗时![]() 小时,结果与甲车同时到达B地.
小时,结果与甲车同时到达B地.
(1)甲车的速度为 千米/时;
(2)求乙车装货后行驶的速度;
(3)乙车出发 小时与甲车相距10千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com