
【题目】如图,在Rt△ABC中,AC=BC=2,将△ABC绕点A逆时针旋转60°,连接BD,则图中阴影部分的面积是( )
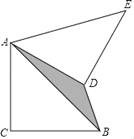
A. 2![]() ﹣2B. 2
﹣2B. 2![]() C.
C. ![]() ﹣1D. 4
﹣1D. 4![]()
【答案】C
【解析】
由旋转的性质可得AB=AE,∠BAE=60°,AD=AC=2,BC=DE=2,可得△ABE是等边三角形,根据“SSS”可证△ADB≌△EDB,可得S△ADB=S△EDB,由S阴影=![]() (S△ABE-S△ADE)可求阴影部分的面积.
(S△ABE-S△ADE)可求阴影部分的面积.
解:如图,连接BE,
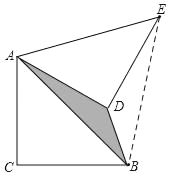
∵在Rt△ABC中,AC=BC=2,
∴AB2=AC2+BC2=8
∵将△ABC绕点A逆时针旋转60°,
∴AB=AE,∠BAE=60°,AD=AC=2,BC=DE=2,
∴△ABE是等边三角形,
∴AB=BE,S△ABE=![]() AB2=2
AB2=2![]() ,
,
∵AB=BE,AD=DE,DB=DB
∴△ADB≌△EDB(SSS)
∴S△ADB=S△EDB,
∴S阴影=![]() (S△ABE﹣S△ADE)
(S△ABE﹣S△ADE)
∴S阴影=![]()
故选:C.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案科目:初中数学 来源: 题型:
【题目】某检修小组从![]() 地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:
地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:![]() )
)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
|
|
|
|
|
|
|
(1)在第__________次记录时距![]() 地最远;
地最远;
(2)求收工时距![]() 地多远?
地多远?
(3)若每千米耗油![]() 升,每升汽油需
升,每升汽油需![]() 元,问检修小组工作一天需汽油费多少元?
元,问检修小组工作一天需汽油费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() ,
,![]() ,
,![]() ,设
,设![]() ,
,![]() ,
,![]() ,……,
,……,![]()
(1)计算![]() ___________,
___________,![]() ____________,
____________,![]() ____________
____________
(2)写出![]() ,
,![]() ,
,![]() ,
,![]() 四者之间的关系,并证明你的结论.
四者之间的关系,并证明你的结论.
(3)根据(2)的结论,直接写出![]() 的值是_____________
的值是_____________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承优秀传统文化,我市组织了一次初三年级1200名学生参加的“汉字听写”大赛,为了更好地了解本次大赛的成绩分布情况,随机抽取了100名学生的成绩(满分50分),整理得到如下的统计图表:
成绩(分) | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | ||
人 数 | 1 | 2 | 3 | 3 | 6 | 7 | 5 | 8 | 15 | 9 | 11 | 12 | 8 | 6 | 4 | ||
成绩分组 | 频数 | 频率 | |||||||||||||||
35≤x<38 | 3 | 0.03 | |||||||||||||||
38≤x<41 | a | 0.12 | |||||||||||||||
41≤x<44 | 20 | 0.20 | |||||||||||||||
44≤x<47 | 35 | 0.35 | |||||||||||||||
47≤x≤50 | 30 | b | |||||||||||||||
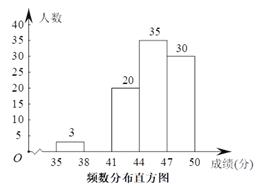
请根据所提供的信息解答下列问题∶
(1)样本的中位数是 分;
(2)频率统计表中a= ,b= ;
(3)请补全频数分布直方图;
(4)请根据抽样统计结果,估计该次大赛中成绩不低于41分的学生有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上,点O为原点,点A对应的数为9,点B对应的数为b,点C在点B右侧,长度为2个单位的线段BC在数轴上移动.
![]()
(1)当b=5时,试求线段AC的长;
(2)当线段BC在数轴上沿射线AO方向移动的过程中,若存在AC﹣OB=![]() AB,求此时满足条件的b值.
AB,求此时满足条件的b值.
(3)当线段BC在数轴上移动时,满足关系式|AC﹣OB|=|AB﹣OC|,则此时的b的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知正方形ABCD的边长为1,点P是AD边上的一个动点,点A关于直线BP的对称点是点Q,连接PQ、DQ、CQ、BQ,设AP=x.
(1)BQ+DQ的最小值是_______,此时x的值是_______;
(2)如图②,若PQ的延长线交CD边于点E,并且∠CQD=90°.
①求证:点E是CD的中点; ②求x的值.
(3)若点P是射线AD上的一个动点,请直接写出当△CDQ为等腰三角形时x的值.
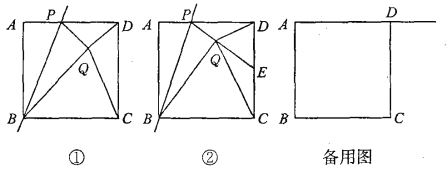
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题
某中学组织七年级师生去春游,一人一座,如果单租45座客车若干辆,则刚好坐满;如果单租60座的客车,则少租一辆,且余15个座位.
(1)求参加春游的师生总人数.
(2)已知一辆45座客车的租金每天250元,一辆60座客车的租金每天300元,问单租哪种客车省钱?
(3)如果同时租用这两种客车,那么两种客车分别租多少辆最省钱?(只写出租车方案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电子厂商设计了一款制造成本为18元新型电子厂品,投放市场进行试销.经过调查,得到每月销售量y(万件)与销售单价x(元)之间的部分数据如下:
销售单价x(元/件) | … | 20 | 25 | 30 | 35 | … |
每月销售量y(万件) | … | 60 | 50 | 40 | 30 | … |
(1)求出每月销售量y(万件)与销售单价x(元)之间的函数关系式.
(2)求出每月的利润z(万元)与销售单x(元)之间的函数关系式.
(3)根据相关部门规定,这种电子产品的销售利润率不能高于50%,而且该电子厂制造出这种产品每月的制造成本不能超过900万元.那么并求出当销售单价定为多少元时,厂商每月能获得最大利润?最大利润是多少?(利润=售价﹣制造成本)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com