
【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根x1、x2 .
(1)求实数k的取值范围.
(2)若方程两实根x1、x2满足x1+x2=﹣x1x2 , 求k的值.
【答案】
(1)
解:∵原方程有两个不相等的实数根,
∴△=(2k+1)2﹣4(k2+1)>0,
解得:k> ![]() ,
,
即实数k的取值范围是k> ![]() ;
;
(2)
解:∵根据根与系数的关系得:x1+x2=﹣(2k+1),x1x2=k2+1,
又∵方程两实根x1、x2满足x1+x2=﹣x1x2,
∴﹣(2k+1)=﹣(k2+1),
解得:k1=0,k2=2,
∵k> ![]() ,
,
∴k只能是2.
【解析】本题考查了根与系数的关系和根的判别式的应用,能正确运用性质进行计算是解此题的关键,题目比较好,难度适中.(1)根据根与系数的关系得出△>0,代入求出即可;(2)根据根与系数的关系得出x1+x2=﹣(2k+1),x1x2=k2+1,根据x1+x2=﹣x1x2得出﹣(2k+1)=﹣(k2+1),求出方程的解,再根据(1)的范围确定即可.
【考点精析】本题主要考查了求根公式和根与系数的关系的相关知识点,需要掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】已知点A(-8,0)及动点P(x,y),且2x-y=-6.设三角形OPA的面积为S.
(1)当x=-2时,点P坐标是____________;
(2)若点P在第二象限,且x为整数时,求y的值;
(3)是否存在第一象限的点P,使得S=12.若存在,求点P的坐标;若不存在,
说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
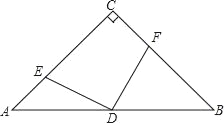
【题目】已知:如图,在△ABC中,∠ACB=90°,AC=BC,D是AB的中点,点E在AC上,点F在BC上,且AE=CF.
(1)求证:DE=DF,DE⊥DF;
(2)若AC=2,求四边形DECF面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
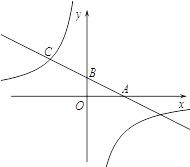
【题目】如图,一次函数的图象与![]() 轴、
轴、![]() 轴分别相交于A、B两点,且与反比例函数的图象在第二象限交于点C.如果点A的坐标为(4,0),OA=2OB,点 B是AC的中点.
轴分别相交于A、B两点,且与反比例函数的图象在第二象限交于点C.如果点A的坐标为(4,0),OA=2OB,点 B是AC的中点.
(1)求点C的坐标;
(2)求一次函数和反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系中,O是坐标原点,点A(2,5)在反比例函数y= ![]() 的图象上.一次函数y=x+b的图象过点A,且与反比例函数图象的另一交点为B.
的图象上.一次函数y=x+b的图象过点A,且与反比例函数图象的另一交点为B.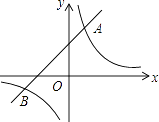
(1)求k和b的值;
(2)设反比例函数值为y1 , 一次函数值为y2 , 求y1>y2时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,BD⊥AD,∠A=45°,E、F分别是AB、CD上的点,且BE=DF,连接EF交BD于O.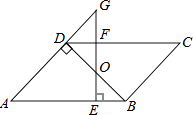
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】历史上的数学巨人欧拉最先把关于x的多项式用记号f(x)来表示.例如f(x)=x2+3x-5,把x=某数时多项式的值用f(某数)来表示.例如x=-1时多项式x2+3x-5的值记为f(-1)=(-1)2+3×(-1)-5=-7.
(1)已知g(x)=-2x2-3x+1,分别求出g(-1)和g(-2);
(2)已知h(x)=ax3+2x2-ax-6,当h(![]() )=a,求a的值;
)=a,求a的值;
(3)已知f(x)=![]() -
-![]() -2(a,b为常数),当k无论为何值,总有f(1)=0,求a,b的值.
-2(a,b为常数),当k无论为何值,总有f(1)=0,求a,b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,动点P从点B出发,沿着B﹣A﹣D在菱形ABCD的边上运动,运动到点D停止,点P′是点P关于BD的对称点,PP′交BD于点M,若BM=x,△OPP′的面积为y,则y与x之间的函数图象大致为( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,动点P从点B出发,沿着B﹣A﹣D在菱形ABCD的边上运动,运动到点D停止,点P′是点P关于BD的对称点,PP′交BD于点M,若BM=x,△OPP′的面积为y,则y与x之间的函数图象大致为( )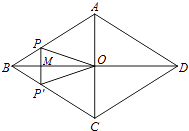
A.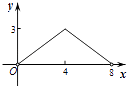
B.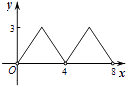
C.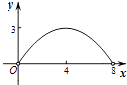
D.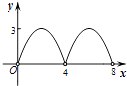
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com