
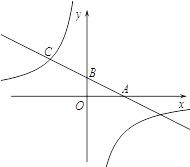
【题目】如图,一次函数的图象与![]() 轴、
轴、![]() 轴分别相交于A、B两点,且与反比例函数的图象在第二象限交于点C.如果点A的坐标为(4,0),OA=2OB,点 B是AC的中点.
轴分别相交于A、B两点,且与反比例函数的图象在第二象限交于点C.如果点A的坐标为(4,0),OA=2OB,点 B是AC的中点.
(1)求点C的坐标;
(2)求一次函数和反比例函数的解析式.
【答案】解:⑴作CD⊥![]() 轴于D,
轴于D,
∴CD∥BO.
∵OA=2OB,
∴OB=2.
∴![]() .
.
∵点B是AC的中点,
∴O是AD的中点.
∴OD=OA=4,CD=2OB=4.
∴点C的坐标为![]() .
.
⑵设反比例函数的解析式为![]() ,
,
∴![]() .
.
∴所求反比例函数的解析式为![]() .
.
设一次函数为![]() ,
,
∵A(4,0),C![]() ,
,
∴![]() 解得:
解得: .
.
∴所求一次函数的解析式为![]() .
.
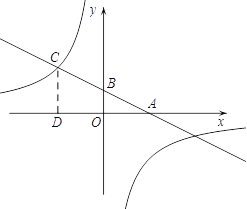
【解析】试题分析:(1)作CD⊥![]() 轴于D,可得CD∥BO.根据点A的坐标为(4,0),OA=2OB,求出B点坐标,根据点B是AC的中点,可知O是AD的中点.即可得到点C的坐标;(2)设反比例函数解析式为
轴于D,可得CD∥BO.根据点A的坐标为(4,0),OA=2OB,求出B点坐标,根据点B是AC的中点,可知O是AD的中点.即可得到点C的坐标;(2)设反比例函数解析式为![]() ,代入C点坐标,解得即可;设一次函数的解析式y=kx+b,将点A、点C的坐标代入,运用待定系数法即可求出一次函数的解析式.
,代入C点坐标,解得即可;设一次函数的解析式y=kx+b,将点A、点C的坐标代入,运用待定系数法即可求出一次函数的解析式.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图所示,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,错误的有( )
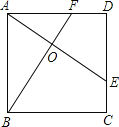
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
下面是一个有关平行四边形和等边三角形的小实验,请根据实验解答问题:
已知在□ABCD中,∠ABC=120°,点D又是等边三角形DEF的一个顶点,DE与AB相交于点M,DF与BC相交于点N(不包括线段的端点).
(1)初步尝试:
如图①,若AB=BC,求证:BD=BM+BN;
(2)探究发现:
如图②,若BC=2AB,过点D作DH⊥BC于点H,求证:∠BDC=90°.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+b的图象经过A(-2,-1),B(1,3)两点,并且交x轴于点C,交y轴于点D.

(1)求该一次函数的解析式;
(2)求点C和点D的坐标;
(3)求△AOB的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A( ![]() ,0),B(0,2),则点B2016的坐标为 .
,0),B(0,2),则点B2016的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+m(m>0)与x轴交于点A(-2,0),直线y=-x+n(n>0)与x轴、y轴分别交于B、C两点,并与直线y=2x+m(m>0)相交于点D,若AB=4.
(1)求点D的坐标;
(2)求出四边形AOCD的面积;
(3)若E为x轴上一点,且△ACE为等腰三角形,直接写出点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根x1、x2 .
(1)求实数k的取值范围.
(2)若方程两实根x1、x2满足x1+x2=﹣x1x2 , 求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com