
【题目】如图,已知抛物线y=ax2+bx+c经过A(﹣3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H.
(1)求该抛物线的解析式;
(2)若点P是该抛物线对称轴l上的一个动点,求△PBC周长的最小值;
(3)如图(2),若E是线段AD上的一个动点( E与A、D不重合),过E点作平行于y轴的直线交抛物线于点F,交x轴于点G,设点E的横坐标为m,△ADF的面积为S.
①求S与m的函数关系式;
②S是否存在最大值?若存在,求出最大值及此时点E的坐标; 若不存在,请说明理由.

【答案】(1)抛物线的解析式为:y=﹣x2﹣2x+3;(2)![]() ;(3)最大值为1,此时点E的坐标为(﹣2,2).
;(3)最大值为1,此时点E的坐标为(﹣2,2).
【解析】(1)根据函数图象经过的三点,用待定系数法确定二次函数的解析式即可;
(2)根据BC是定值,得到当PB+PC最小时,△PBC的周长最小,根据点的坐标求得相应线段的长即可;
(3)设点E的横坐标为m,表示出E(m,2m+6),F(m,﹣m2﹣2m+3),最后表示出EF的长,从而表示出S于m的函数关系,然后求二次函数的最值即可.
解:(1)由题意可知: 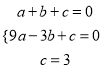 ,解得:
,解得: 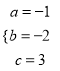 ,
,
∴抛物线的解析式为:y=﹣x2﹣2x+3;
(2)∵△PBC的周长为:PB+PC+BC
∵BC是定值,
∴当PB+PC最小时,△PBC的周长最小,
∵点A、点B关于对称轴I对称,
∴连接AC交l于点P,即点P为所求的点
∵AP=BP
∴△PBC的周长最小是:PB+PC+BC=AC+BC
∵A(﹣3,0),B(1,0),C(0,3),
∴AC=3![]() ,BC=
,BC=![]() ;
;
(3)①∵抛物线y=﹣x2﹣2x+3顶点D的坐标为(﹣1,4)
∵A(﹣3,0)
∴直线AD的解析式为y=2x+6
∵点E的横坐标为m,
∴E(m,2m+6),F(m,﹣m2﹣2m+3)
∴EF=﹣m2﹣2m+3﹣(2m+6)=﹣m2﹣4m﹣3
∴S=S△DEF+S△AEF=EFGH+EFAC=EFAH=(﹣m2﹣4m﹣3)×2=﹣m2﹣4m﹣3;
②S=﹣m2﹣4m﹣3
=﹣(m+2)2+1;
∴当m=﹣2时,S最大,最大值为1
此时点E的坐标为(﹣2,2).
“点睛”此题主要考查了待定系数法求二次函数解析式以及二次函数的最值,根据点的坐标表示出线段的长是表示出三角形的面积的基础.


科目:初中数学 来源: 题型:
【题目】判断题,对的画“√”错的画“×”
(1)对角线互相垂直的四边形是菱形(______)
(2)一条对角线垂直另一条对角线的四边形是菱形(_____)
(3)对角线互相垂直且平分的四边形是菱形(_____)
(4)对角线相等的四边形是菱形(_____)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).

(1)请用列表的方法表示出上述游戏中两数和的所有可能的结果;
(2)分别求出李燕和刘凯获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句正确的是( )
A. 线段绕着它的中点旋转180°后与原线段重合,那么线段是中心对称图形
B. 正三角形绕着它的三边中线的交点旋转120°后与原图形重合,则正三角形是中心对称图形
C. 正方形绕着它的对角线交点旋转90°后与原图形重合,则正方形是中心对称图形
D. 正五角星绕着它的中心旋转72°后与原图形重合,则正五角星是中心对称图形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算正确的是( )
A. (x+y)2=x2+y2B. (﹣x+y)2=x2+2xy+y2
C. (x﹣2y)(x+2y)=x2﹣2y2D. (x﹣1)(﹣x﹣1)=1﹣x2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com