
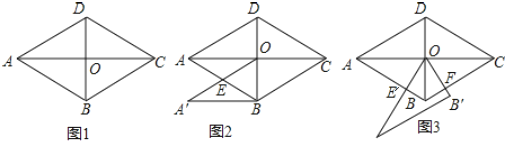
【题目】如图1,菱形ABCD,![]() ,
,![]() ,连接对角线AC、BD交于点O,
,连接对角线AC、BD交于点O,
![]() 如图2,将
如图2,将![]() 沿DB平移,使点D与点O重合,求平移后的
沿DB平移,使点D与点O重合,求平移后的![]() 与菱形ABCD重合部分的面积.
与菱形ABCD重合部分的面积.
![]() 如图3,将
如图3,将![]() 绕点O逆时针旋转交AB于点
绕点O逆时针旋转交AB于点![]() ,交BC于点F,
,交BC于点F,
![]() 求证:
求证:![]() ;
;
![]() 求出四边形
求出四边形![]() 的面积.
的面积.
【答案】![]() 证明见解析
证明见解析![]()
【解析】
(1)先判断出△ABD是等边三角形,进而判断出△EOB是等边三角形,即可得出结论;
(2)先判断出 ≌△OBF,再利用等式的性质即可得出结论;
(3)借助①的结论即可得出结论.
![]() 四边形为菱形,
四边形为菱形,![]() ,
,
![]() ,
,
![]() 为等边三角形,
为等边三角形,
![]() ,
,![]() ,
,
∵AD//A′O,
∴∠A′OB=60°,
![]() 为等边三角形,边长
为等边三角形,边长![]() ,
,
![]() 重合部分的面积:
重合部分的面积:![]() ,
,
![]() 在图3中,取AB中点E,
在图3中,取AB中点E,
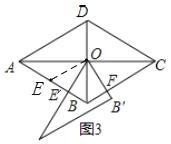
由![]() 知,∠EOB=60°,∠E′OF=60°,
知,∠EOB=60°,∠E′OF=60°,
∴∠EOE′=∠BOF,
又∵EO=BO,∴∠OEE′=∠OBF=60°,
∴△OEE′≌△OBF,
∴EE′=BF,
∴BE′+BF=BE′+EE′=BE=2;
![]() 由
由![]() 知,在旋转过程中始终有△OEE′≌△OBF,
知,在旋转过程中始终有△OEE′≌△OBF,
∴S△OEE′=S△OBF,
![]() S四边形OE′BF =
S四边形OE′BF =![]() .
.


科目:初中数学 来源: 题型:
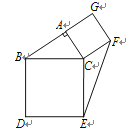
【题目】如图,在△ABC中,∠BAC=90°,分别以AC,BC为边长,在三角形外作正方形ACFG和正方形BCED.若AC=4,AB=6,则EF=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在坐标平面内,已知点A(0,3)、B(6,5),

(1)连接AB,在x轴上确定点P,使PA=PB(用尺规作图,保留作图痕迹,不写作法),并求出P点坐标;
(2)点Q是x轴上的动点,求点Q与A、B两点的距离之和的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大树AB与大数CD相距13m,小华从点B沿BC走向点C,行走一段时间后他到达点E,此时他仰望两棵大树的顶点A和D,两条视线的夹角正好为90°,且EA=ED.已知大树AB的高为5m,小华行走的速度为1m/s,小华行走到点E的时间是( )

A. 13s B. 8s C. 6s D. 5s
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大树AB与大数CD相距13m,小华从点B沿BC走向点C,行走一段时间后他到达点E,此时他仰望两棵大树的顶点A和D,两条视线的夹角正好为90°,且EA=ED.已知大树AB的高为5m,小华行走的速度为1m/s,小华行走到点E的时间是( )

A. 13s B. 8s C. 6s D. 5s
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中是真命题的是( )
A. 有两边和其中一边的对角对应相等的两个三角形全等
B. 两条平行直线被第三条直线所截,则一组同旁内角的平分线互相垂直
C. 三角形的一个外角等于两个内角的和
D. 等边三角形既是中心对称图形,又是轴对称图形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某农户发展养禽业,准备利用现有的34米长的篱笆靠墙AB(墙长为25米)围成一个面积为120平方米的长方形养鸡场,这个养鸡场的长和宽各是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.

(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:两个二次项系数之和为1,对称轴相同,且图象与y轴交点也相同的二次函数互为友好同轴二次函数![]() 例如:
例如:![]() 的友好同轴二次函数为
的友好同轴二次函数为![]() .
.
![]() 请你分别写出
请你分别写出![]() ,
,![]() 的友好同轴二次函数;
的友好同轴二次函数;
![]() 满足什么条件的二次函数没有友好同轴二次函数?满足什么条件的二次函数的友好同轴二次函数是它本身?
满足什么条件的二次函数没有友好同轴二次函数?满足什么条件的二次函数的友好同轴二次函数是它本身?
![]() 如图,二次函数
如图,二次函数![]() :
:![]() 与其友好同轴二次函数
与其友好同轴二次函数![]() 都与y轴交于点A,点B、C分别在
都与y轴交于点A,点B、C分别在![]() 、
、![]() 上,点B,C的横坐标均为
上,点B,C的横坐标均为![]() ,它们关于
,它们关于![]() 的对称轴的对称点分别为
的对称轴的对称点分别为![]() ,
,![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,CB.
,CB.
![]() 若
若![]() ,且四边形
,且四边形![]() 为正方形,求m的值;
为正方形,求m的值;
![]() 若
若![]() ,且四边形
,且四边形![]() 的邻边之比为1:2,直接写出a的值.
的邻边之比为1:2,直接写出a的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com