练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    —抛物线与x轴的交点是A(－2，0)，B(1，0)，且经过点C(2，8)．

        (1)求该抛物线的解析式；

    (2)求该抛物线的顶点坐标．


    解：(1)设这个抛物线的解析式为y=ax2＋bx＋c．将A(－2，0)，B(1，0)，C(2，8)三点代入，得解这个方程组，得∴所求抛物线的解析式为y＝2x2＋2x－4．  (2)∵y=2x2＋2x－4＝2(x2＋x－2)=2(x＋)2－，∴该抛物线的顶点坐标为(－，－)． 


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    一组数据按从小到大的顺序排列为1，2，3，x，4，5，若这组数据的中位数为3，则这组数据的方差是          .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知二次函数y＝x2－4x＋5的顶点坐标为(　　)

    A．(－2，－1)  B．(2,1)  C．(2，－1)  D．(－2,1)

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    二次函数y=ax2+bx+c，b2=ac，且x=0时y=-4则（  ）

        A．y最大=-4     B．y最小=-4    C．y最大=-3     D．y最小=3

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知抛物线y＝ax2+bx+c的对称轴为x=2，且经过点(1，4)和点(5，0)，则该抛物线的解析式为    ．

      

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知函数y=（x﹣m）（x﹣n）（其中m＜n）的图象如图所示，则一次函数y=mx+n与反比例函数y=的图象可能是（　　）

    　A．BCD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某玩具厂计划生产一种玩具熊猫，每日最高产量为40只，且每日产出的产品全部售出，已知生产x只熊猫的成本为R元，售价为每只P元，且R，P与x之间的函数关系式分别为R＝500＋30x，P＝170－2x.

        (1)当日产量为多少只时，每日获得的利润为1750元?

    (2)当日产量为多少只时，每日可获得最大利润?最大利润是多少元?

    查看答案和解析>>

    科目：初中数学 来源： 题型：


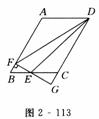
    如图2 - 113所示，在ABCD中，AB＝4，BC＝3，∠BAD＝120°，E为BC上一动点(不与B重合)，作EF⊥AB于F，延长FE与DC的延长线交于点G，设BE＝x，△DEF的面积为S．

        (1)求证△BEF∽△CEG；

        (2)用x表示S的函数关系式，并写出x的取值范围；

    (3)当E运动到何处时，S有最大值，最大值为多少?

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图3－33所示，弦CD垂直于⊙O的直径AB，垂足为E，且CD＝，BD＝，则AB的长为    (    )

             A．2         　　　　　   B．3

             C．4　       　　　　　　 D．5

    查看答案和解析>>

    同步练习册答案