Question

4．在平面直角坐标系中，点A（-3，0），B（4，0），C（0，3），∠ABC的角平分线BD交AC于D，点P在射线BD上移动，点E在x轴上移动．若BC=5，则PA+PE的最小值是$\frac{21}{5}$．

Answer 1

分析 延长BC到A′，使BA′=BA，则点A′是点A关于直线BD的对称点，于是得到BA′=BA=7，连接A′E，交射线BD于P，则P就是使PA+PE的最小值的点，它的位置随点E的移动而变化，根据“垂线段最短”得：当A′E⊥x轴时，A′E最短，即PA+PE最小，通过△BOC∽△BA′E′，列比例式即可得到结论．

解答 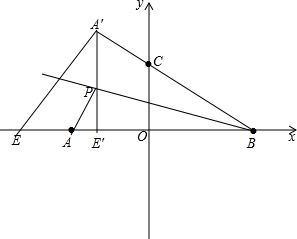解：延长BC到A′，使BA′=BA，
∵∠ABC的角平分线BD交AC于D，
∴点A′是点A关于直线BD的对称点，
∴BA′=BA=7，
连接A′E，交射线BD于P，
则P就是使PA+PE的最小值的点，
它的位置随点E的移动而变化，
且PA+PE=A′E，
根据“垂线段最短”得：当A′E⊥x轴时，A′E最短，即PA+PE最小，
∵A′E′⊥x轴，OC⊥x轴，
∴OC∥A′E′，
∴△BOC∽△BA′E′，
∴$\frac{A′E′}{OC}=\frac{A′B}{BC}$，
即$\frac{A′E′}{3}=\frac{7}{5}$，
∴A′E′=$\frac{21}{5}$，即PA+PE的最小值=$\frac{21}{5}$．
故答案为：$\frac{21}{5}$．

点评 此题主要考查轴对称--最短路线问题，坐标与图形的性质，相似三角形的判定和性质，正确的作出图形是解题的关键．