
����Ŀ����������L��y=ax2+bx+c��a��b��c�dz�����abc��0����ֱ��l������y���ϵ�һ��P����������L�Ķ���Q��ֱ��l�ϣ���ƴ�ֱ��l���������L���С�һ��һ·����ϵ����ʱ��ֱ��l����������L�ġ����ߡ���������L����ֱ��l�ġ�·�ߡ���
��1����ֱ��y=mx+1��������y=x2��2x+n���С�һ��һ·����ϵ����m��n��ֵ��
��2����ij��·�ߡ�L�Ķ����ڷ���������y=![]() ��ͼ���ϣ����ġ����ߡ�l�Ľ���ʽΪy=2x��4����ˡ�·�ߡ�L�Ľ���ʽ��
��ͼ���ϣ����ġ����ߡ�l�Ľ���ʽΪy=2x��4����ˡ�·�ߡ�L�Ľ���ʽ��
��3��������k����![]() ��k��2ʱ����������L��y=ax2+��3k2��2k+1��x+k�ġ����ߡ�l��x�ᣬy����Χ�ɵ������������ȡֵ��Χ��
��k��2ʱ����������L��y=ax2+��3k2��2k+1��x+k�ġ����ߡ�l��x�ᣬy����Χ�ɵ������������ȡֵ��Χ��
���𰸡���1��m��ֵΪ��1��n��ֵΪ1����2��y=2��x+1��2��6��y=��![]() ��x��3��2+2����3��
��x��3��2+2����3��![]() ��S��
��S��![]() ��
��
��������
�����������1��ȷ��ֱ��y=mx+1��y��Ľ������꣬������������߽���ʽ�м������n��ֵ���ٸ��������ߵĽ���ʽ�ҳ��������꣬�������ֱ�߽���ʽ�м��ɵó����ۣ���2��ȷ��ֱ���뷴��������ͼ��Ľ������꣬�ɴ���������ߵĽ���ʽ������ֱ�ߵĽ���ʽ�ҳ�ֱ����x��Ľ������꣬������������߽���ʽ�м��ɵó����ۣ���3���������߽���ʽ�ҳ���������y��Ľ������꣬�ٸ��������ߵĽ���ʽ�ҳ��䶥�����꣬�����������ϴ���ϵ�������ɵó���������߶�Ӧ�ġ����ߡ�l�Ľ���ʽ���ҳ���ֱ����x��y��Ľ������꣬��������ε�����ҳ����S����k�Ĺ�ϵ�ϣ��ɶ��κ��������ʼ��ɵó����ۣ�
�����������1����ֱ��y=mx+1��x=0����y=1��
��ֱ����y��Ľ���Ϊ��0��1����
����0��1������������y=x2��2x+n��
��n=1��
�������ߵĽ���ʽΪy=x2��2x+1=��x��1��2��
�������ߵĶ�������Ϊ��1��0����
������1��0�����뵽ֱ��y=mx+1�У�
�ã�0=m+1����ã�m=��1��
��m��ֵΪ��1��n��ֵΪ1��
��2����y=2x��4���뵽y=![]() ���У�
����
2x��4=![]() ����2x2��4x��6=0��
����2x2��4x��6=0��
��ã�x1=��1��x2=3��
��á�·�ߡ�L�Ķ�������Ϊ����1����6������3��2����
����ߡ�l��y=2x��4��x=0����y=��4��
�ࡰ·�ߡ�L��ͼ�������0����4����
��á�·�ߡ�L�Ľ���ʽΪy=m��x+1��2��6��y=n��x��3��2+2��
��������4=m��0+1��2��6��4=n��0��3��2+2��
��ã�m=2��n=��![]() ��
��
��ˡ�·�ߡ�L�Ľ���ʽΪy=2��x+1��2��6��y=��![]() ��x��3��2+2��
��x��3��2+2��
��3����������L��y=ax2+��3k2��2k+1��x+k��x=0����y=k��
������������y��Ľ���Ϊ��0��k����
������L��y=ax2+��3k2��2k+1��x+k�Ķ�������Ϊ����![]() ��
��![]() ����
����
�衰���ߡ�l�Ľ���ʽΪy=px+k��
�ߵ�����![]() ��
��![]() ����y=px+k�ϣ�
����y=px+k�ϣ�
��![]() =��p
=��p![]() +k��
+k��
��ã�p=![]() ��
��
�ࡰ���ߡ�l�Ľ���ʽΪy=![]() x+k��
x+k��
��ࡰ���ߡ�l��y=![]() x+k��y=0����0=
x+k��y=0����0=![]() x+k��
x+k��
��ã�x=��![]() ��
��
�������ߡ�l��x��Ľ���Ϊ����![]() ��0������y��Ľ���Ϊ��0��k����
��0������y��Ľ���Ϊ��0��k����
�ࡰ���ߡ�l��x�ᣬy����Χ�ɵ����������S=![]() |��
|��![]() |��|k|��
|��|k|��
��![]() ��k��2��
��k��2��
��![]() ��
��![]() ��2��
��2��
��S=![]() =
=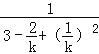 =
=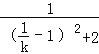 ��
��
��![]() =1ʱ��S�����ֵ�����ֵΪ
=1ʱ��S�����ֵ�����ֵΪ![]() ��
��
��![]() =2ʱ��S����Сֵ����СֵΪ
=2ʱ��S����Сֵ����СֵΪ![]() ��
��
��������L��y=ax2+��3k2��2k+1��x+k�ġ����ߡ�l��x�ᣬy����Χ�ɵ������������ȡֵ��ΧΪ![]() ��S��
��S��![]() ��
��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
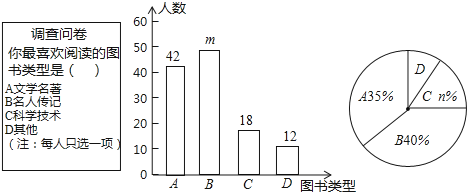
����Ŀ��Ϊ������ѧ�����Ķ�ϰ�ߣ�ijУ��չ�ˡ������飬���ɳ���ϵ�л����������һ��ͼ�飬����ǰ ����ѧ��ϲ���Ķ���ͼ�����ͽ����˳������飬�����������ݻ��Ƴ�������������ͳ��ͼ����ͼ��ʾ������ͳ��ͼ���ṩ����Ϣ���ش��������⣺
��1�����ε��鹲����� ��ѧ��������ͳ��ͼ�е�m= ��n= .
��2����֪��У����960��ѧ��������Ƹ�Уϲ���Ķ���A����ͼ���ѧ��Լ�ж����ˣ�
��3��ѧУҪ�ٰ����֪ʶ���������꣨1����Ҫ�ڰ༶��ʤ��2��1Ů�����ѡ��2�˲�������ѡ�͵���������ѧ��Ϊ1��1Ů�ĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b��ͼ��ֱ��뷴��������y=![]() ��ͼ���ڵ�һ�����ڵ�A��4��3������y��ĸ����ύ�ڵ�B����OA=OB��
��ͼ���ڵ�һ�����ڵ�A��4��3������y��ĸ����ύ�ڵ�B����OA=OB��
��1������y=kx+b��y=![]() �ı���ʽ��
�ı���ʽ��
��2����֪��C��0��5�������ڸ�һ�κ���ͼ����ȷ��һ��M��ʹ��MB=MC�����ʱ��M�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Rt��ABC�У���C=90�㣬a��b=3��4�����ü��������㣬��A�Ķ�������ȷ��1�㣩��������
A.30��
B.37��
C.38��
D.39��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ�����ǰ�ABC�У���A=30�㣬BC��1.������ֱ�Ƕ���C��ʱ����תһ����![]() ��
��![]() ��
��![]() �����õ�Rt��
�����õ�Rt��![]() .
.
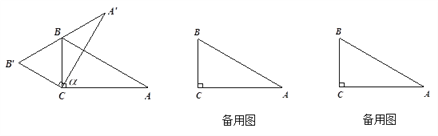
��1����ͼ������![]() ������Bʱ������ת��
������Bʱ������ת��![]() �Ķ�����
�Ķ�����
��2�������ǰ���ת�Ĺ����У���![]() ��AB����ֱ�߽��ڵ�D������ D��DE��
��AB����ֱ�߽��ڵ�D������ D��DE��![]() ��
��![]() ���ڵ�E������BE.
���ڵ�E������BE.
�ٵ�![]() ʱ����AD=
ʱ����AD=![]() ��BE=
��BE=![]() ����
����![]() ��
��![]() ֮��ĺ�������ʽ���Ա���
֮��ĺ�������ʽ���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�ڵ�![]() ʱ����AD�ij�.
ʱ����AD�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����MON=90�㣬��A��B�ֱ���OM��ON���˶��������O�غϣ��� 

��1����BC�ǡ�ABN��ƽ���ߣ�BC�ķ������ӳ������BAO��ƽ���߽����D�� ������BAO=60�㣬���D=�㣮
�ڲ��룺��D�Ķ����Ƿ���A��B���ƶ������仯����˵������ ��
��2������ABC= ![]() ��ABN����BAD=
��ABN����BAD= ![]() ��BAO�����D=�㣮
��BAO�����D=�㣮
��3����������MON=90�㡱��Ϊ����MON=����0�㣼����180�㣩������ABC= ![]() ��ABN����BAD=
��ABN����BAD= ![]() ��BAO�������������䣬���D=�㣨�ú�����n�Ĵ���ʽ��ʾ��
��BAO�������������䣬���D=�㣨�ú�����n�Ĵ���ʽ��ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=kx+b��k��0����ͼ���뷴��������![]() ��m��0����ͼ����A��B���㣬��x�ύ��C�㣬��A������Ϊ��n��6������C������Ϊ����2��0������tan��ACO=2��
��m��0����ͼ����A��B���㣬��x�ύ��C�㣬��A������Ϊ��n��6������C������Ϊ����2��0������tan��ACO=2��
��1����÷�����������һ�κ����Ľ���ʽ��
��2�����B�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����x��3����2x+1��=2x2+mx+n����m��n��ֵ�ֱ��ǣ� ��
A.5����3
B.��5��3
C.��5����3
D.5��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�E��BC�ϣ�BE=2��CE=1����P��BD�ϣ���PE��PC�ĺ͵���СֵΪ �� 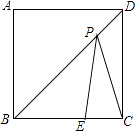
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com