
【题目】直角三角板ABC中,∠A=30°,BC=1.将其绕直角顶点C逆时针旋转一个角![]() (
(![]() 且
且![]() ),得到Rt△
),得到Rt△![]() .
.
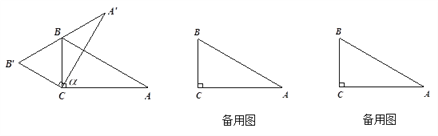
(1)如图,当边![]() 经过点B时,求旋转角
经过点B时,求旋转角![]() 的度数;
的度数;
(2)在三角板旋转的过程中,边![]() 与AB所在直线交于点D,过点 D作DE∥
与AB所在直线交于点D,过点 D作DE∥![]() 交
交![]() 边于点E,联结BE.
边于点E,联结BE.
①当![]() 时,设AD=
时,设AD=![]() ,BE=
,BE=![]() ,求
,求![]() 与
与![]() 之间的函数解析式及自变量
之间的函数解析式及自变量![]() 的取值范围;
的取值范围;
②当![]() 时,求AD的长.
时,求AD的长.
【答案】(1)![]() =
=![]() ;(2)①
;(2)① ![]() (0﹤
(0﹤![]() ﹤2);②AD=1或
﹤2);②AD=1或![]() .
.
【解析】(1)由旋转的性质可得出∠α=∠B′CB=60°;
(2)①当0°<α<90°时,点D在AB边上(如图).根据平行线DE∥A'B'分线段成比例知![]() 、及由旋转性质可知,CA=CA',CB=CB',∠ACD=∠BCE由此证明△CAD∽△CBE;根据相似三角形的对应边成比例、直角三角形的性质及∠A=30°求得y=
、及由旋转性质可知,CA=CA',CB=CB',∠ACD=∠BCE由此证明△CAD∽△CBE;根据相似三角形的对应边成比例、直角三角形的性质及∠A=30°求得y=![]() x(0<x<2);
x(0<x<2);
②先求得△ABC的面积,再由△CAD∽△CBE,求得BE,分情况讨论:当点D在AB边上时,AD=x,BD=AB-AD=2-x;当点D在AB的延长线上时,AD=x,BD=x-2.
解:(1)在Rt△![]() 中,∵∠A=30°,∴
中,∵∠A=30°,∴![]() .
.
由旋转可知:![]() ,
,![]() ,
,![]()
∴△![]() 为等边三角形.
为等边三角形.
∴![]() =
=![]() .
.
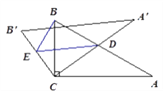
(2)① 当![]() 时,点D在AB边上(如图).
时,点D在AB边上(如图).
∵ DE∥![]() ,∴
,∴ ![]() .
.
由旋转性质可知,CA =![]() ,CB=
,CB=![]() , ∠ACD=∠BCE.
, ∠ACD=∠BCE.
∴ ![]() ∴
∴ ![]() .
.
∴ △CAD∽△CBE.
∴![]() .∵∠A=30° ∴
.∵∠A=30° ∴![]()
![]() .
.
∴![]() (0﹤
(0﹤![]() ﹤2)
﹤2)
②当![]() 时,点D在AB边上
时,点D在AB边上
AD=x,![]() ,∠DBE=90°.
,∠DBE=90°.
此时,![]() .
.
当S =![]() 时,
时,![]() .整理,得
.整理,得 ![]() .
.
解得 ![]() ,即AD=1.
,即AD=1.
当![]() 时,点D在AB的延长线上(如图).
时,点D在AB的延长线上(如图).
仍设AD=x,则![]() ,∠DBE=90°.
,∠DBE=90°.
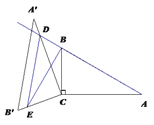
![]() .
.
当S =![]() 时,
时,![]() .
.
整理,得 ![]() .
.
解得 ![]() ,
,![]() (负值,舍去).
(负值,舍去).
即![]() .
.
综上所述:AD=1或![]() .
.
“点睛”本题主要考查旋转、全等三角形、解直角三角形、平行线分线段成比例等知识.解决本题的关键是结合图形,分类讨论.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是40cm.求: 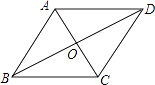
(1)两条对角线AC、BD的长度;
(2)菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线L:y=ax2+bx+c(a,b,c是常数,abc≠0)与直线l都经过y轴上的一点P,且抛物线L的顶点Q在直线l上,则称此直线l与该抛物线L具有“一带一路”关系.此时,直线l叫做抛物线L的“带线”,抛物线L叫做直线l的“路线”.
(1)若直线y=mx+1与抛物线y=x2﹣2x+n具有“一带一路”关系,求m,n的值;
(2)若某“路线”L的顶点在反比例函数y=![]() 的图象上,它的“带线”l的解析式为y=2x﹣4,求此“路线”L的解析式;
的图象上,它的“带线”l的解析式为y=2x﹣4,求此“路线”L的解析式;
(3)当常数k满足![]() ≤k≤2时,求抛物线L:y=ax2+(3k2﹣2k+1)x+k的“带线”l与x轴,y轴所围成的三角形面积的取值范围.
≤k≤2时,求抛物线L:y=ax2+(3k2﹣2k+1)x+k的“带线”l与x轴,y轴所围成的三角形面积的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中装有红色、白色玻璃球共40个,除颜色外其他完全相同,小明通过多次摸球试验后发现,其中摸到红色球的频率稳定在0.15左右,则口袋中红色球可能有__________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两个变量x和y,它们之间的3组对应值如下表所示:
x | -1 | 0 | 1 |
y | -1 | 1 | 3 |
则y与x之间的函数关系式可能是( )
A. y=x B. y=2x+1 C. y=x2+x+1 D. y=3x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com