Question

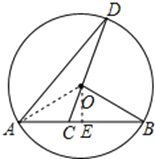
【题目】如图，已知AB是⊙O的弦，OB = 2，∠B = 30°，C是弦AB上任意一点（不与点A、B重合），连接CO并延长CO交⊙O于点D，连接AD．

（1）弦长AB = ____________（结果保留根号）；

（2）当∠D = 20°时，求∠BOD的度数；

（3）当AC的长度为多少时，以点A、C、D为顶点的三角形与以B、C、O为顶点的三角形相似？请写出解答过程．

Answer 1

【答案】（1）2（2）100°（3）AC=．

【解析】试题分析：（1）过点O作OE⊥AB于E，则AE=BE=AB，在Rt△BOE中，利用∠B的余弦可求出BE的长，然后可得出AB的长；（2）连接OA，根据OA=OD=OB,可得∠D =∠DAO =" 20°," ∠B=∠BAO = 30°,然后可求出∠DAB = 50°,再利用圆周角定理可得∠BOD=2∠DAB = 100°；（3）利用三角形的外角的性质可得∠BCO=

∠A+∠D，然后分析可得出只能是△DAC∽△BOC，此时∠DCA=∠BCO=90°，∠DAC=60°，在Rt△BOE中，利用∠DAC的三角函数值可求出AC的长．

试题解析：解：（1）过点O作OE⊥AB于E，

则AE=BE=AB，∠OEB=90°，

∵OB=2，∠B=30°，∴BE=OBcos∠B=2×=，

∴AB=2；故答案为：2；

（2）连接OA，

∵OA=OB，OA=OD，∴∠BAO=∠B，∠DAO=∠D，

∴∠DAB=∠BAO+∠DAO=∠B+∠D，

又∵∠B=30°，∠D=20°，

∴∠DAB=50°，

∴∠BOD=2∠DAB=100°；

（3）∵∠BCO=∠A+∠D，

∴∠BCO＞∠A，∠BCO＞∠D，

∴要使△DAC与△BOC相似，只能∠DCA=∠BCO=90°，

此时∠BOC=60°，∠BOD=120°，∴∠DAC=60°，∴△DAC∽△BOC，

∵∠BCO=90°，即OC⊥AB，∴AC=AB=．

∴当AC的长度为时，以A、C、D为顶点的三角形与以B、C、0为顶点的三角形相似．