
【题目】如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:(1)AE=BF;(2)AE⊥BF;(3)AO=OE;(4) ![]() 中正确的有( )
中正确的有( )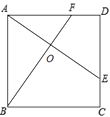
A. 4个
B. 3个
C. 2个
D. 1个
【答案】B
【解析】解:∵四边形ABCD是正方形,
∴AB=AD,∠BAF=∠ADE=90°.
∵CE=DF,∴AF=DE.
∴△ABF≌△DAE.
∴AE=BF;
∠AFB=∠AED.
∵∠AED+∠DAE=90°,
∴∠AFB+∠DAE=90°,
∴∠AOF=90°,即AE⊥BF;
S△AOB=S△ABF-S△AOF , S四边形DEOF=S△ADE-S△AOF ,
∵△ABF≌△DAE,
∴S△ABF=S△ADE ,
∴S△AOB=S四边形DEOF .
故正确的有 (1)、(2)、(4).
【考点精析】利用正方形的性质对题目进行判断即可得到答案,需要熟知正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
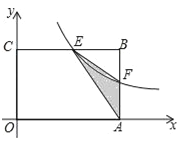
【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数![]() (k>0)的图象与BC边交于点E.
(k>0)的图象与BC边交于点E.
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D、E两点的坐标. 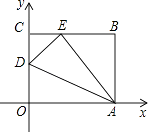
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班将举行“防溺水安全知识竞赛”活动,班主任安排班长购买奖品,下面是班长买回奖品时与班主任的对话情况:
班长:买了两种不同的奖品共50件,单价分别为3元和5元,我领了200元,现在找回35元
班主任:你肯定搞错了!
班长:哦!我把自己口袋里的15元一起当作找回的钱款了.
班主任:这就对了!
请根据上面的信息,解决下列问题:
(1)计算两种奖品各买了多少件?
(2)请你解释:班长为什么不可能找回35元?
查看答案和解析>>
科目:初中数学 来源: 题型:
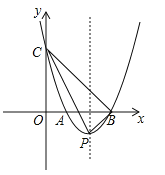
【题目】如图,在平面直角坐标系中,抛物线![]() 经过点(﹣1,8)并与x轴交于点A,B两点,且点B坐标为(3,0).
经过点(﹣1,8)并与x轴交于点A,B两点,且点B坐标为(3,0).
(1)求抛物线的解析式;
(2)若抛物线与y轴交于点C,顶点为点P,求△CPB的面积.
注:抛物线![]() (a≠0)的顶点坐标是(
(a≠0)的顶点坐标是(![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴的原点为O,如图所示,点A表示﹣2,点B表示3,请回答下列问题:
(1)数轴是什么图形?数轴在原点右边的部分(包括原点)是什么图形?数轴上表示不小于﹣2,且不大于3的部分是什么图形?请你分别给它们取一个合适的名字;
(2)请你在射线AO上再标上一个点C(不与A点重合),那么表示点C的值x的取值范围是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
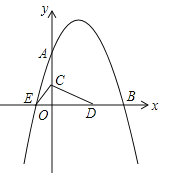
【题目】如图,已知抛物线![]() 与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
(1)直接写出抛物线的解析式: ;
(2)求△CED的面积S与D点运动时间t的函数解析式;当t为何值时,△CED的面积最大?最大面积是多少?
(3)当△CED的面积最大时,在抛物线上是否存在点P(点E除外),使△PCD的面积等于△CED的最大面积?若存在,求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com