【题目】知识迁移

我们知道，函数的图像是由二次函数的图像向右平移m个单位，再向上平移n个单位得到．类似地，函数的图像是由反比例函数的图像向右平移m个单位，再向上平移n个单位得到，其对称中心坐标为（m，n）．

理解应用

函数的图像可以由函数的图像向右平移 个单位，再向上平移 个单位得到，其对称中心坐标为 ．

灵活运用

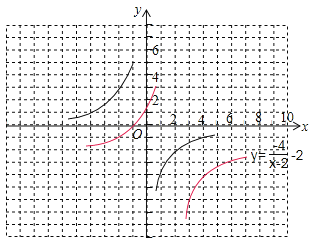
如图，在平面直角坐标系xOy中，请根据所给的的图像画出函数的图像，并根据该图像指出，当x在什么范围内变化时，≥？

实际应用

某老师对一位学生的学习情况进行跟踪研究．假设刚学完新知识时的记忆存留量为1．新知识学习后经过的时间为x，发现该生的记忆存留量随x变化的函数关系为；若在（≥4）时进行一次复习，发现他复习后的记忆存留量是复习前的2倍（复习时间忽略不计），且复习后的记忆存量随x变化的函数关系为．如果记忆存留量为时是复习的“最佳时机点”，且他第一次复习是在“最佳时机点”进行的，那么当x为何值时，是他第二次复习的“最佳时机点”？

参考答案：

【答案】（1）理解应用：1，1，（1，1）；（2）灵活应用：当﹣2≤x＜2时；（3）实际应用：当x=12时，是他第二次复习的“最佳时机点”．

【解析】

试题分析：理解应用：由“知识迁移”得到双曲线的图象平移变换的规律：上加下减．由此得到答案：

灵活应用：由平移规律作出图象；

实际应用：先求出第一次复习的“最佳时机点”（4，1），然后带入y2，求出解析式，然后再求出第二次复习的“最佳时机点”．

试题解析：理解应用：根据“知识迁移”易得，函数的图象可由函数的图象向右平移 1个单位，再向上平移 1个单位得到，其对称中心坐标为 （1，1）．故答案为：1，1，（1，1）；

灵活应用：将的图象向右平移2个单位，然后再向下平移两个单位，即可得到函数的图象，其对称中心是（2，﹣2）．图象如图所示：

由y=﹣1，得，解得x=﹣2．

由图可知，当﹣2≤x＜2时，y≥﹣1；

实际应用：

当x=t时，，则由=，解得：t=4，即当t=4时，进行第一次复习，复习后的记忆存留量变为1，∴点（4，1）在函数的图象上，则，解得：a=﹣4，∴，当=，解得：x=12，即当x=12时，是他第二次复习的“最佳时机点”．

关闭