
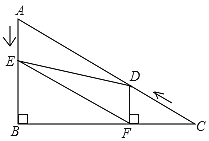
����Ŀ����ͼ����Rt��ABC�У���B=90����AC=10����C=30������D�ӵ�C������CA������ÿ��2����λ���ȵ��ٶ����A�����˶���ͬʱ��E�ӵ�A������AB������ÿ��1����λ���ȵ��ٶ����B�����˶���������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶������D��E�˶���ʱ����t��t��0���룬����D��DF��BC�ڵ�F������DE��EF��
��1����֤���ı���AEFD��ƽ���ı��Σ�
��2����tΪ��ֵʱ����DEF�ǵȱ������Σ�˵�����ɣ�
��3����tΪ��ֵʱ����DEFΪֱ�������Σ�����ֱ��д��t��ֵ��
���𰸡���1������������2����tΪ![]() ʱ����DEF�ǵȱ������Σ�����������3����tΪ
ʱ����DEF�ǵȱ������Σ�����������3����tΪ![]() ��4ʱ����DEFΪֱ�������Σ�
��4ʱ����DEFΪֱ�������Σ�
��������
��1����Rt��CDF�У�����30�ȽǵĶԱߵ���б�ߵ�һ�룬���ɵó�DF�ij�������ý⣻
��2����֪����DEF�ǵȱ�������ʱ����EDA�ǵȱ������Σ��ɡ�A=60���ɵó�AD=AE�������ɵó�����t��һԪһ�η��̣���֮���ɵó����ۣ�
��3����֪����DEFΪֱ��������ʱ����EDA��ֱ�������Σ��֡�AED=90���͡�ADE=90������������ǣ�����30�ȽǵĶԱߵ���б�ߵ�һ�룬�ɵó�����t��һԪһ�η��̣���֮���ɵó����ۣ�
�⣺��1��֤��������DFC�У���DFC=90������C=30����DC=2t��
��DF=t��
�֡�AE=t��
��AE=DF��
��AE��DF��
���ı���AEFD��ƽ���ı��Σ�
��2�����ı���AEFD��ƽ���ı��Σ�
�൱��DEF�ǵȱ�������ʱ����EDA�ǵȱ������Σ�
�ߡ�A=90��-��C=60����
��AD=AE��
��AE=t��AD=AC-CD=10-2t��
��t=10-2t��
��t=![]() ��
��
�൱tΪ![]() ʱ����DEF�ǵȱ������Σ�
ʱ����DEF�ǵȱ������Σ�
��3�����ı���AEFD��ƽ���ı��Σ�
�൱��DEFΪֱ��������ʱ����EDA��ֱ�������Σ�
����AED=90��ʱ��AD=2AE����10-2t=2t��
��ã�t=![]() ��
��
����ADE=90��ʱ��AE=2AD����t=2��10-2t����
��ã�t=4��
������������tΪ![]() ��4ʱ����DEFΪֱ�������Σ�
��4ʱ����DEFΪֱ�������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в���
������ȫƽ����ʽ��������ʽx2+bx+c����Ϊ(x+m)2+n����ʽ��Ȼ����(x+m)2��0�Ϳ��������ʽx2+bx+c����Сֵ.
���⣺��x2��12x+37����Сֵ.
�⣺x2��12x+37��x2��2x��6+62��62+37��(x��6)2+1,
��Ϊ����xȡ��ֵ��(x��6)2���ǷǸ�������(x��6)2��0,
����(x��6)2+1��1.
���Ե�x=6ʱ��x2��12x+37����Сֵ����Сֵ��1.
�����������ϣ�����������⣺
(1)���:x2��8x+_________=(x��_______)2,
(2)��x2+10x��2����Ϊ(x+m)2+n����ʽ�������x2+10x��2����Сֵ,
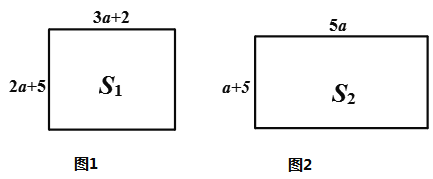
(3)��ͼ����ʾ�ij����α߳��ֱ���2a+5��3a+2�����ΪS1����ͼ����ʾ�ij����α߳��ֱ���5a��a+5�����ΪS2. �ԱȽ�S1��S2�Ĵ�С����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����C���߶�AB��һ�㣬M���߶�AC���е㣬N���߶�BC���е㣮
(1)���AB��10cm��AM��3cm����CN�ij���
(2)���MN��6cm����AB�ij���
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
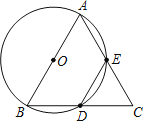
����Ŀ����ͼ������ABC�У�AB��BC��2����ABΪֱ���ġ�O�ֱ�BC��AC�ڵ�D��E���ҵ�DΪBC���е㣮
��1����֤����ABCΪ�ȱ������Σ�
��2����DE�ij���
��3�����߶�AB���ӳ������Ƿ����һ��P��ʹ��PBD�ա�AED�������ڣ������PB�ij����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����̳�����A��B�����ͺż����������ּ������Ľ����۸�ֱ�Ϊÿ̨30Ԫ��40Ԫ. �̳�����5̨A�ͺź�1̨B�ͺż��������ɻ�����76Ԫ������6̨A�ͺź�3̨B�ͺż��������ɻ���120Ԫ.
��1�����̳�����A��B�����ͺż����������ۼ۸�ֱ��Ƕ���Ԫ��������=���ۼ۸��������۸�
��2���̳����ò�����2500Ԫ���ʽ�A��B�����ͺż�������70̨����������Ҫ����A�ͺŵļ���������̨��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�Ƶ�B˳ʱ����ת60������DBE����C�Ķ�Ӧ��Eǡ������AB�ӳ����ϣ�����AD�����н���һ����ȷ���ǣ���
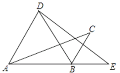
A. AD��BC B. ��CBE=��C C. ��ABD=��E D. AD=BC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�ĶԽ���AC��BD����ڵ�O��EF����O������AD��BC�ֱ��ཻ��E��F����AB=4��BC=5��OE=1.5�����ı���EFCD���ܳ��ǣ� ��

A.16B.14C.12D.10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���![]() �У�
��![]() ��
��![]() ��
�� ![]() ��
��![]() ��
�� ![]() ������P�ӵ�D���������߶�
������P�ӵ�D���������߶� ![]() �ķ�����ÿ��2����λ�����ٶ��˶�������Q�ӵ� C���������߶�
�ķ�����ÿ��2����λ�����ٶ��˶�������Q�ӵ� C���������߶� ![]() ����ÿ��1����λ�����ٶ����
����ÿ��1����λ�����ٶ����![]() �˶�����P��
�˶�����P��![]() �ֱ�ӵ�D��Cͬʱ����������
�ֱ�ӵ�D��Cͬʱ����������![]() �˶�����
�˶����� ![]() ʱ����Q��ֹ֮ͣ�˶������˶���ʱ��Ϊt�룩.
ʱ����Q��ֹ֮ͣ�˶������˶���ʱ��Ϊt�룩.

��1���� ![]() ʱ����
ʱ���� ![]() �������
�������
��2�����ı���![]() Ϊƽ���ı��Σ����˶�ʱ��
Ϊƽ���ı��Σ����˶�ʱ��![]() .
.
��3���� ![]() Ϊ��ֵʱ���� B��P��QΪ������������ǵ��������Σ�
Ϊ��ֵʱ���� B��P��QΪ������������ǵ��������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Ϊ����һ��ɽ��CF�ĸ߶ȣ�����ɽ��ij��ɽ�»���ΪAB��BC���Σ�ÿһ��ɽ�½����ǡ�ֱ���ģ�����³�AB=800�ף�BC=200�ף��½ǡ�BAF=30�㣬��CBE=45�㣮
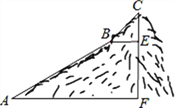
��1����AB��ɽ�µĸ߶�EF��
��2����ɽ��ĸ߶�CF����![]() 1.414��CF�����ȷ���ף�
1.414��CF�����ȷ���ף�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com