
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
, ![]() ,
,![]() ,
, ![]() ,动点P从点D出发,沿线段
,动点P从点D出发,沿线段 ![]() 的方向以每秒2个单位长的速度运动;动点Q从点 C出发,在线段
的方向以每秒2个单位长的速度运动;动点Q从点 C出发,在线段 ![]() 上以每秒1个单位长的速度向点
上以每秒1个单位长的速度向点![]() 运动;点P,
运动;点P,![]() 分别从点D,C同时出发,当点
分别从点D,C同时出发,当点![]() 运动到点
运动到点 ![]() 时,点Q随之停止运动,设运动的时间为t秒).
时,点Q随之停止运动,设运动的时间为t秒).

(1)当 ![]() 时,求
时,求 ![]() 的面积;
的面积;
(2)若四边形![]() 为平行四边形,求运动时间
为平行四边形,求运动时间![]() .
.
(3)当 ![]() 为何值时,以 B、P、Q为顶点的三角形是等腰三角形?
为何值时,以 B、P、Q为顶点的三角形是等腰三角形?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)过点![]() 作
作![]() 于
于![]() ,则PM=DC,当t=2时,算出BQ,求出面积即可;(2)当四边形
,则PM=DC,当t=2时,算出BQ,求出面积即可;(2)当四边形![]() 是平行四边形时,
是平行四边形时,![]() ,即
,即![]() ,解出即可;(3)以 B、P、Q为顶点的三角形是等腰三角形,分三种情况,①
,解出即可;(3)以 B、P、Q为顶点的三角形是等腰三角形,分三种情况,①![]() ,②
,②![]() ,③
,③![]() 分别求出t即可.
分别求出t即可.
解 :(1)过点![]() 作
作![]() 于
于![]() ,则四边形
,则四边形![]() 为矩形.
为矩形.
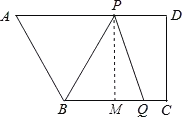
∴![]() ,
,
∵![]() ,
,
当t=2时,则BQ=14,
则![]() =
=![]() ×14×12=84;
×14×12=84;
(2)当四边形![]() 是平行四边形时,
是平行四边形时,![]() ,
,
即![]()
解得:![]()
∴当![]() 时,四边形
时,四边形![]() 是平行四边形.
是平行四边形.
(3)由图可知,CM=PD=2t,CQ=t,若以B、P、Q为顶点的三角形是等腰三角形,可以分为以下三种情况:
①若![]() ,在
,在![]() 中,
中,![]() ,由
,由![]() 得
得![]() 解得:
解得:![]() ;
;
②若![]() ,在
,在![]() 中,
中,![]() ,由
,由![]() 得
得![]() ,即
,即![]() ,
,
此时,![]() ,
,
所以此方程无解,所以![]() ;
;
③若![]() ,由
,由![]() 得
得![]() ,
,
得 ![]() ,
,![]() (不合题意,舍去);
(不合题意,舍去);
综上所述,当![]() 或
或![]() 时,以B、P、Q为顶点的三角形是等腰三角形.
时,以B、P、Q为顶点的三角形是等腰三角形.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
|
|
|
|
|
| ··· |
![]() 可求得
可求得![]() ,第
,第![]() 个格子中的数为 ;
个格子中的数为 ;
![]() 判断:前
判断:前![]() 个格子中所填整数之和是否可能为
个格子中所填整数之和是否可能为![]() 若能,求出
若能,求出![]() 的值,若不可能,请说明理由;
的值,若不可能,请说明理由;
![]() 如果
如果![]() ,
,![]() 为前
为前![]() 格子中的任意两个数,那么所有
格子中的任意两个数,那么所有![]() 的和可以通过计算
的和可以通过计算
![]() 得到,若
得到,若![]() span>,
span>,![]() 为前
为前![]() 格子中的任意两个数,则所有
格子中的任意两个数,则所有![]() 的的和为
的的和为
查看答案和解析>>
科目:初中数学 来源: 题型:
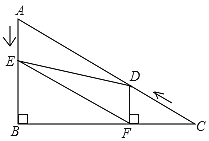
【题目】如图,在Rt△ABC中,∠B=90°,AC=10,∠C=30°,点D从点C出发沿CA方向以每秒2个单位长度的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长度的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t(t>0)秒,过点D作DF⊥BC于点F,连接DE、EF.
(1)求证:四边形AEFD是平行四边形;
(2)当t为何值时,△DEF是等边三角形?说明理由;
(3)当t为何值时,△DEF为直角三角形?(请直接写出t的值)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C、D均在⊙O上,FB与⊙O相切于点B,AB与CF交于点G,OA⊥CF于点E,AC∥BF.
(1)求证:FG=FB.
(2)若tan∠F=![]() ,⊙O的半径为4,求CD的长.
,⊙O的半径为4,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
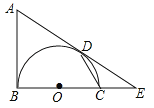
【题目】(2016浙江省丽水市)如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD,BC的延长线相交于点E.
(1)求证:AD是半圆O的切线;
(2)连结CD,求证:∠A=2∠CDE;
(3)若∠CDE=27°,OB=2,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要建一个面积为150 m2的矩形养鸡场,为了节约材料,养鸡场的一边沿用原来的一堵墙,墙长为a m,其余三边用竹篱笆围成,已知竹篱笆的长为35 m.
(1)如果a=40,那么养鸡场的长和宽各为多少米?
(2)如果a是一个可以变化的量,那么墙的长度a对所建的养鸡场有怎样的影响?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)由大小相同的小立方块搭成的几何体如图1,请在图2的方格中画出该几何体的俯视图和左视图.
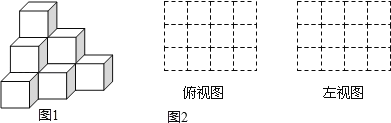
(2)用小立方体搭一个几何体,使得它的俯视图和左视图与你在方格中所画的一致,则这样的几何体最少要 个小立方块,最多要 个小立方块.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,点A的坐标为(m,0),点B的坐标为(0,n),其中m=![]() ,
,![]() =0,将三角形BOA沿x轴的正方向向右平移10个单位长度得到三角形CDE,连接BC.
=0,将三角形BOA沿x轴的正方向向右平移10个单位长度得到三角形CDE,连接BC.
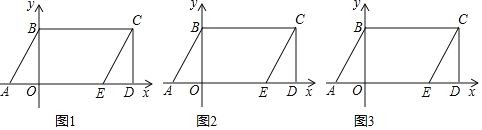
(1)如图1,分别求点C、点E的坐标;
(2)点P自点C出发,以每秒1个单位长度沿线段CB运动,同时点Q自点O出发,以每秒2个单位长度沿线段OE运动,连接AP、BQ,点Q运动至点E时,点P同时停止运动.设运动时间t(秒),三角形ABQ的面积与三角形APB的面积的和为s(平方单位),求s与t的关系式,并直接写出t的取值范围;
(3)在(2)的条件下,BP:QE=8:3,此时将线段PQ向左平移2个单位长度得到线段P'Q'(点P'与点P对应),线段P′Q'再向下平移2个单位长度得到线段MN(点M与点P'对应),线段MN交x轴于点G,点H在线段OA上,OH=![]() OG,过点H作HR⊥OA,交AB于点R,求点R的坐标.
OG,过点H作HR⊥OA,交AB于点R,求点R的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com