
【题目】阅读下列材料
利用完全平方公式,将多项式x2+bx+c变形为(x+m)2+n的形式,然后由(x+m)2≥0就可求出多项式x2+bx+c的最小值.
例题:求x2-12x+37的最小值.
解:x2-12x+37=x2-2x·6+62-62+37=(x-6)2+1,
因为不论x取何值,(x-6)2总是非负数,即(x-6)2≥0,
所以(x-6)2+1≥1.
所以当x=6时,x2-12x+37有最小值,最小值是1.
根据上述材料,解答下列问题:
(1)填空:x2-8x+_________=(x-_______)2,
(2)将x2+10x-2变形为(x+m)2+n的形式,并求出x2+10x-2的最小值,
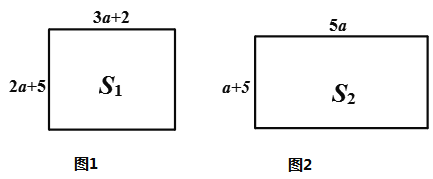
(3)如图①所示的长方形边长分别是2a+5、3a+2,面积为S1:如图②所示的长方形边长分别是5a、a+5,面积为S2. 试比较S1与S2的大小,并说明理由.
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
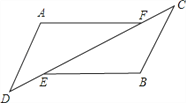
【题目】如图△ADF和△BCE中,∠A=∠B,点D、E、F、C在同﹣直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF。
(1)请用其中两个关系式作为条件,另一个作为结论,写出所有你认为正确的命题.(用序号写出命题书写形式,如:如果①、②,那么③)
(2)选择(1)中你写出的一个命题,说明它正确的理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条不完整的数轴上从左到右有点![]() ,其中点
,其中点![]() 到点
到点![]() 的距离为3,点
的距离为3,点![]() 到点
到点![]() 的距离为7,如图所示:设点
的距离为7,如图所示:设点![]() 所对应的数的和是
所对应的数的和是![]() .
.
(1)若以![]() 为原点,则
为原点,则![]() 的值是 .
的值是 .
(2)若原点![]() 在图中数轴上,且点
在图中数轴上,且点![]() 到原点
到原点![]() 的距离为4,求
的距离为4,求![]() 的值.
的值.
(3)动点![]() 从
从![]() 点出发,以每秒2个单位长度的速度向终点
点出发,以每秒2个单位长度的速度向终点![]() 移动,动点
移动,动点![]() 同时从
同时从![]() 点出发,以每秒1个单位的速度向终点
点出发,以每秒1个单位的速度向终点![]() 移动,当几秒后,
移动,当几秒后,![]() 两点间的距离为2?(直接写出答案即可)
两点间的距离为2?(直接写出答案即可)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热[此过程中水温y(℃)与开机时间x(分)满足一次函数关系],当加热到100℃时自动停止加热,随后水温开始下降[此过程中水温y(℃)与开机时间x(分)成反比例关系],当水温降至20℃时,饮水机又自动开始加热…,重复上述程序(如图所示),根据图中提供的信息,解答下列问题:
(1)当0≤x≤8时,求水温y(℃)与开机时间x(分)的函数关系式;
(2)求图中t的值;
(3)若小明在通电开机后即外出散步,请你预测小明散步45分钟回到家时,饮水机内的温度约为多少℃?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)材料1:一般地,n个相同因数a相乘:![]() 记为
记为 ![]() 如
如![]() ,此时,3叫做以2为底的8的对数,记为log28(即log28=3).那么,log39=________,
,此时,3叫做以2为底的8的对数,记为log28(即log28=3).那么,log39=________,![]() =________;
=________;
(2)材料2:新规定一种运算法则:自然数1到n的连乘积用n!表示,例如:1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1=24,…在这种规定下,请你解决下列问题:
①算5!=________;
②已知x为整数,求出满足该等式的![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2﹣4x+2)(x2﹣4x+6)+4进行因式分解的过程.
解:设x2﹣4x=y
原式=(y+2)(y+6)+4(第一步)
=y2+8y+16(第二步)
=(y+4)2(第三步)
=(x2﹣4x+4)2(第四步)
回答下列问题:
(1)该同学因式分解的结果是否彻底 _________ .(填“彻底”或“不彻底”)
若不彻底,请直接写出因式分解的最后结果 _________ .
(2)请你模仿以上方法尝试对多项式(x2﹣2x)(x2﹣2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
|
|
|
|
|
| ··· |
![]() 可求得
可求得![]() ,第
,第![]() 个格子中的数为 ;
个格子中的数为 ;
![]() 判断:前
判断:前![]() 个格子中所填整数之和是否可能为
个格子中所填整数之和是否可能为![]() 若能,求出
若能,求出![]() 的值,若不可能,请说明理由;
的值,若不可能,请说明理由;
![]() 如果
如果![]() ,
,![]() 为前
为前![]() 格子中的任意两个数,那么所有
格子中的任意两个数,那么所有![]() 的和可以通过计算
的和可以通过计算
![]() 得到,若
得到,若![]() span>,
span>,![]() 为前
为前![]() 格子中的任意两个数,则所有
格子中的任意两个数,则所有![]() 的的和为
的的和为
查看答案和解析>>
科目:初中数学 来源: 题型:
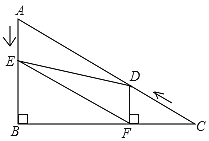
【题目】如图,在Rt△ABC中,∠B=90°,AC=10,∠C=30°,点D从点C出发沿CA方向以每秒2个单位长度的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长度的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t(t>0)秒,过点D作DF⊥BC于点F,连接DE、EF.
(1)求证:四边形AEFD是平行四边形;
(2)当t为何值时,△DEF是等边三角形?说明理由;
(3)当t为何值时,△DEF为直角三角形?(请直接写出t的值)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com