
����Ŀ��������ijͬѧ�Զ���ʽ��x2��4x+2����x2��4x+6��+4������ʽ�ֽ�Ĺ��̣�
�⣺��x2��4x=y
ԭʽ=��y+2����y+6��+4����һ����
=y2+8y+16���ڶ�����
=��y+4��2����������
=��x2��4x+4��2�����IJ���
�ش��������⣺
��1����ͬѧ��ʽ�ֽ�Ľ���Ƿ���_________������������������������������
�������ף���ֱ��д����ʽ�ֽ���������_________����
��2������ģ�����Ϸ������ԶԶ���ʽ��x2��2x����x2��2x+2��+1������ʽ�ֽ⣮

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
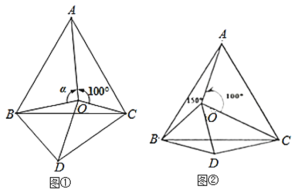
����Ŀ����ͼ�٣���![]() �ǵȱ�
�ǵȱ�![]() ��һ�㣬
��һ�㣬![]() ��
��![]() ����
����![]() Ϊ�����ȱ�������
Ϊ�����ȱ�������![]() ������
������![]() ��
��
��1����֤��![]() ��
��
��2����![]() ʱ����ͼ�ڣ������ж�
ʱ����ͼ�ڣ������ж�![]() ����״����˵�����ɣ�
����״����˵�����ɣ�
��3����![]() �Ƕ��ٶ�ʱ��
�Ƕ��ٶ�ʱ��![]() �ǵ��������Σ���д�����̣�
�ǵ��������Σ���д�����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в���
������ȫƽ����ʽ��������ʽx2+bx+c����Ϊ(x+m)2+n����ʽ��Ȼ����(x+m)2��0�Ϳ��������ʽx2+bx+c����Сֵ.
���⣺��x2��12x+37����Сֵ.
�⣺x2��12x+37��x2��2x��6+62��62+37��(x��6)2+1,
��Ϊ����xȡ��ֵ��(x��6)2���ǷǸ�������(x��6)2��0,
����(x��6)2+1��1.
���Ե�x=6ʱ��x2��12x+37����Сֵ����Сֵ��1.
�����������ϣ�����������⣺
(1)���:x2��8x+_________=(x��_______)2,
(2)��x2+10x��2����Ϊ(x+m)2+n����ʽ�������x2+10x��2����Сֵ,
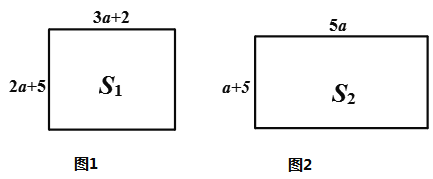
(3)��ͼ����ʾ�ij����α߳��ֱ���2a+5��3a+2�����ΪS1����ͼ����ʾ�ij����α߳��ֱ���5a��a+5�����ΪS2. �ԱȽ�S1��S2�Ĵ�С����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
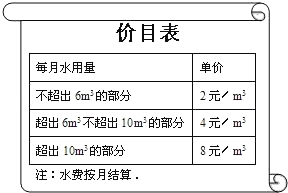
����Ŀ��Ϊ�˼�ǿ����Ľ�ˮ��ʶ����������ˮ��Դ��ij�в��ü۸�����ֶδﵽ��ˮ��Ŀ�ģ���������ˮ�շѼ۸����Ŀ����
��ij������1�·���ˮ8m3����Ӧ��ˮ�ѣ�Ԫ
2��6+4��(8-6)=20
(1)���û�����2�·���ˮ12.5m3����Ӧ��ˮ���� ��Ԫ��
(2)���û�����3��4�·ݹ���ˮ20m3(4�·���ˮ������3�·�)������ˮ��64Ԫ����û�����3��4�·ݸ���ˮ���������ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��У������4Ԫ/���ļ۸�ij��Ʒ��Ϊ�ƶ�����Ʒ���������ۼ۸Ը���Ʒ�����������飮����ÿ�������ͬ�����ۼۣ��������ܽ��Ϊ��ֵ������ij�����Ʒ���ۼ�Ϊ6Ԫ/��ʱ��������Ϊ50����
(1)�����Ʒ���ۼ�ΪxԪ/��ʱ��������Ϊy������д��y��x�ĺ�������ʽ(����д��x��ȡֵ��Χ)��
(2)�����п���ѧ��������ʵ�ʣ��ƻ�������Ʒÿ�����������Ϊ60Ԫ�������Ʒ���ۼ�Ӧ��Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˷ḻ������ijУ������һЩƹ�����ĺ�ƹ����ij�̳�����һ��ƹ�����ĺ�ƹ����ƹ������ÿ������80Ԫ��ƹ����ÿ�ж���20Ԫ��������ڡ��ڼ��̳�������չ���������ڼ���ͻ��ṩ�����Żݷ���.
����һ����һ��ƹ��������һ��ƹ����
��������ƹ�����ĺ�ƹ�������۵�90%���
ijУҪ�����̳�����ƹ������20����ƹ����![]() ��(
��(![]() >20������)��
>20������)��
��1����������һ�����踶�� Ԫ(�ú�![]() ����ʽ��ʾ��Ҫ����)�� ���������������踶�� Ԫ(�ú�
����ʽ��ʾ��Ҫ����)�� ���������������踶�� Ԫ(�ú�![]() ����ʽ��ʾ��Ҫ����).
����ʽ��ʾ��Ҫ����).
��2����![]() 30��ͨ������˵����ʱ�����ַ��������Ϊ���㣿
30��ͨ������˵����ʱ�����ַ��������Ϊ���㣿
��3����![]() 30ʱ�����ܸ���һ�ָ�ΪʡǮ�Ĺ�������д����Ĺ�����
30ʱ�����ܸ���һ�ָ�ΪʡǮ�Ĺ�������д����Ĺ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����C���߶�AB��һ�㣬M���߶�AC���е㣬N���߶�BC���е㣮
(1)���AB��10cm��AM��3cm����CN�ij���
(2)���MN��6cm����AB�ij���
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�ĶԽ���AC��BD����ڵ�O��EF����O������AD��BC�ֱ��ཻ��E��F����AB=4��BC=5��OE=1.5�����ı���EFCD���ܳ��ǣ� ��

A.16B.14C.12D.10
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com