
【题目】如图,平行四边形ABCD的对角线AC、BD相较于点O,EF过点O,且与AD、BC分别相交于E、F,若AB=4,BC=5,OE=1.5,则四边形EFCD的周长是( )

A.16B.14C.12D.10
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①b2﹣4ac<0;②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;③2a+b=0;④当y>0时,x的取值范围是﹣1<x<3;⑤当x>0时,y随x增大而减小.其中结论正确的个数是( )
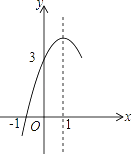
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O交CA于点E,点G是AD的中点.
(1)求证:GE是⊙O的切线;
(2)若AC⊥BC,且AC=8,BC=6,求切线GE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民用电的电价实行阶梯收费,收费标准如下表:
一户居民每月用电量x(单位:度) | 电费价格(单位:元/度) |
0<x≤200 | 0.48 |
200<x≤400 | 0.53 |
x>400 | 0.78 |
七月份是用电高峰期,李叔计划七月份电费支出不超过200元,直接写出李叔家七月份最多可用电的度数是( )
A. 100B. 396C. 397D. 400
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】诗词是我国古代文化中的瑰宝,某市教育主管部门为了解本市初中生对诗词的学习情况,举办了一次“中华诗词”背诵大赛,随机抽取了部分同学的成绩(x为整数,总分100分),绘制了如下尚不完整的统计图表.
组别 | 成绩分组(单位:分) | 频数 |
A | 50≤x<60 | 40 |
B | 60≤x<70 | a |
C | 70≤x<80 | 90 |
D | 80≤x<90 | b |
E | 90≤x<100 | 100 |
合计 | c |
根据以上信息解答下列问题:
(1)统计表中a= ,b= ,c= ;
(2)扇形统计图中,m的值为 ,“E”所对应的圆心角的度数是 (度);
(3)若参加本次大赛的同学共有4000人,请你估计成绩在80分及以上的学生大约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=100°,∠BCD=70°,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,求∠B的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
《张丘建算经》是一部数学问题集,其内容、范围与《九章算术》相仿.其中提出并解决了一个在数学史上非常著名的不定方程问题,通常称为“百鸡问题”:“今有鸡翁一值钱五,鸡母一值钱三,鸡雏三值钱一,凡百钱买鸡百只,问鸡翁、母、雏各几何.”
译文:公鸡每只值五文钱,母鸡每只值三文钱,小鸡每三只值一文钱,现在用一百文钱买一百只鸡,问这一百只鸡中,公鸡、母鸡、小鸡各有多少只?结合你学过的知识,解决下列问题:
(1)若设公鸡有x只,母鸡有y只,
①则小鸡有______只,买小鸡一共花费______文钱;(用含x,y的式子表示)
②根据题意列出一个含有x,y的方程:______;
(2)若对“百鸡问题”增加一个条件:公鸡数量是母鸡数量的3倍,求此时公鸡、母鸡、小鸡各有多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长方形ABCD中,AB=CD=7cm,AD=BC=5cm,∠A=∠B=∠C=∠D=90°,点E在线段AB上以lcms的速度由点A向点B运动,与此同时点F在线段BC上由点B向点C运动,设运动的时间均为ts.
(1)若点F的运动速度与点E的运动速度相等,当t=2时:
①判断△BEF与△ADE是否全等?并说明理由;
②求∠EDF的度数.
(2)如图2,将图1中的“长方形ABCD”改为“梯形ABCD”,且∠A=∠B=70°,AB=7cm,AD=BC=5cm,其他条件不变.设点F的运动速度为xcm/s.是否存在x的值,使得△BEF与△ADE全等?若存在,直接写出相应的x及t的值;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com