
【题目】如图1,长方形ABCD中,AB=CD=7cm,AD=BC=5cm,∠A=∠B=∠C=∠D=90°,点E在线段AB上以lcms的速度由点A向点B运动,与此同时点F在线段BC上由点B向点C运动,设运动的时间均为ts.
(1)若点F的运动速度与点E的运动速度相等,当t=2时:
①判断△BEF与△ADE是否全等?并说明理由;
②求∠EDF的度数.
(2)如图2,将图1中的“长方形ABCD”改为“梯形ABCD”,且∠A=∠B=70°,AB=7cm,AD=BC=5cm,其他条件不变.设点F的运动速度为xcm/s.是否存在x的值,使得△BEF与△ADE全等?若存在,直接写出相应的x及t的值;若不存在,请说明理由.

【答案】(1)①△BEF≌△ADE;②由①得DE=EF,∠BEF=∠ADE;(2)存在,①如图2,当△DAE≌△EBF时,x=1,t=2;②如图3,当△ADE≌△BFE时,AE=BE,AD=BF,x=![]() ,t=
,t=![]() .
.
【解析】
![]() 根据SAS证明:
根据SAS证明:![]() ≌
≌![]() ;
;![]() 由
由![]() :
:![]() ≌
≌![]() 得
得![]() ,
,![]() ,证明
,证明![]() 是等腰直角三角形可得结论;
是等腰直角三角形可得结论;![]() 分两种情况:
分两种情况:![]() 如图2,当
如图2,当![]() ≌
≌![]() 时,
时,![]() 如图3,当
如图3,当![]() ≌
≌![]() 时,分别根据
时,分别根据![]() ,
,![]() ,列方程组可得结论.
,列方程组可得结论.
解:(1)①△BEF≌△ADE,理由如:
当t=2时,AE=BF=2,
∴BE=AB-AD=7-2=5,
∵AD=5,
∴BE=AD,
∵∠A=∠B=90°,
∴△BEF≌△ADE;
②由①得DE=EF,∠BEF=∠ADE,
∵∠A=90°,
∴∠ADE+∠AED=90°,
∴∠BEF+∠AED=90°,
∴∠DEF=180°-(∠BEF+∠AED)=90°,
∵DE=EF
∴∠EDF=∠EFD,
∵∠EDF+∠EFD=90°,
∴∠EDF=45°;
(2)存在,
①如图2,当△DAE≌△EBF时,
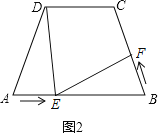
∴AD=BE,AE=BF,
则![]()
∴x=1,t=2;
②如图3,当△ADE≌△BFE时,AE=BE,AD=BF,
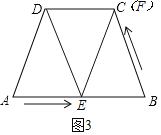
则![]() ,
,
∴x=![]() ,t=
,t=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线AC、BD相较于点O,EF过点O,且与AD、BC分别相交于E、F,若AB=4,BC=5,OE=1.5,则四边形EFCD的周长是( )

A.16B.14C.12D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A,B两个黑布袋,A布袋中有两个完全相同的小球,分别标有数字1和2.B 布袋中有三个完全相同的小球,分别标有数字﹣1,﹣2和﹣3.小明从A布袋中随机取出一个小球,记录其标有的数字为x,再从B布袋中随机取出一个小球,记录其标有的数字为y,这样就确定点Q的一个坐标为(x,y).
(1)用列表或画树状图的方法写出点Q的所有可能坐标;
(2)求点Q落在直线y=﹣x﹣1上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
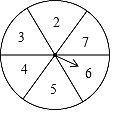
【题目】如图,现有一个转盘被平均分成6等份,分别标有数字2、3、4、5、6、7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字,求:
(1)转到数字10是______(从“不确定事件”“必然事件”“不可能事件”选一个填入);
(2)转动转盘,转出的数字大于3的概率是______;
(3)现有两张分别写有3和4的卡片,要随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.
①这三条线段能构成三角形的概率是多少?
②这三条线段能构成等腰三角形的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】龙人文教用品商店欲购进![]() 、
、![]() 两种笔记本,用160元购进的
两种笔记本,用160元购进的![]() 种笔记本与用240元购进的
种笔记本与用240元购进的![]() 种笔记本数量相同,每本
种笔记本数量相同,每本![]() 种笔记本的进价比每本
种笔记本的进价比每本![]() 种笔记本的进价贵10元.
种笔记本的进价贵10元.
(1)求![]() 、
、![]() 两种笔记本每本的进价分别为多少元?
两种笔记本每本的进价分别为多少元?
(2)若该商店准备购进![]() 、
、![]() 两种笔记本共100本,且购买这两种笔记本的总价不超过2650元,则至少购进
两种笔记本共100本,且购买这两种笔记本的总价不超过2650元,则至少购进![]() 种笔记本多少本?
种笔记本多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车制造厂开发一款新式电动汽车,计划一年生产安装![]() 辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人.他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:
辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人.他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:![]() 名熟练工和
名熟练工和![]() 名新工人每月可安装
名新工人每月可安装![]() 辆电动汽车;
辆电动汽车;![]() 名熟练工和
名熟练工和![]() 名新工人每月可安装
名新工人每月可安装![]() 辆电动汽车.
辆电动汽车.
(1)每名熟练工和新工人每月分别可以安装多少辆电动汽车?
(2)如果工厂招聘![]() 名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?
名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在△ABC中,∠A![]() ,P是BC边上的一点,
,P是BC边上的一点,![]() ,
,![]() 是点P关于AB、AC的对称点,连结
是点P关于AB、AC的对称点,连结![]() ,分别交AB、AC于点D、E.
,分别交AB、AC于点D、E.
①若![]() ,求
,求![]() 的度数;
的度数;
②请直接写出∠A与![]() 的数量关系:___________________________;
的数量关系:___________________________;
(2)如图2,在△ABC中,若∠BAC![]() ,用三角板作出点P关于AB、AC的对称点
,用三角板作出点P关于AB、AC的对称点![]() 、
、![]() ,(不写作法,保留作图痕迹),试判断点
,(不写作法,保留作图痕迹),试判断点![]() ,
,![]() 与点A是否在同一直线上,并说明理由.
与点A是否在同一直线上,并说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,若抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B也在抛物线L1上(点A与点B不重合),我们定义:这样的两条抛物L1,L2互为“友好”抛物线,可见一条抛物线的“友好”抛物线可以有多条.
(1)如图2,已知抛物线L3:y=2x2-8x+4与y轴交于点C,试求出点C关于该抛物线对称轴对称的点D的坐标;
(2)请求出以点D为顶点的L3的友好抛物线L4的解析式,并指出L3与L4中y同时随x增大而增大的自变量的取值范围;
(3)若抛物y=a1 (x-m) 2+n的任意一条友好抛物线的解析式为y=a2 (x-h) 2+k,请写出a1与a2的关系式,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com