
【题目】已知下面三组数值:①![]() ②
②![]() ③
③![]() 其中是方程组
其中是方程组![]() 的解的是( )
的解的是( )
A. ① B. ② C. ③ D. 都不是
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=26°,∠C=70°,AD平分∠BAC,
AE⊥BC于点E,EF⊥AD于点F.
(1)求∠DAC的度数;
(2)求∠DEF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(3,2)、(﹣1,0),若将线段BA绕点B顺时针旋转90°得到线段BA′,则点A′的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大润发超市在销售某种进货价为20元/件的商品时,以30元/件售出,每天能售出100件.调查表明:这种商品的售价每上涨1元/件,其销售量就将减少2件.
(1)为了实现每天1600元的销售利润,超市应将这种商品的售价定为多少?
(2)设每件商品的售价为x元,超市所获利润为y元. ①求y与x之间的函数关系式;
②物价局规定该商品的售价不能超过40元/件,超市为了获得最大的利润,应将该商品售价定为多少?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题。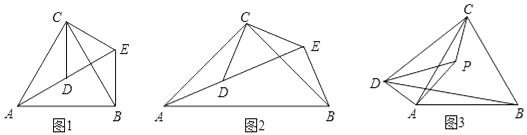
(1)问题发现:如图1,△ACB和△DCE均为等边三角形,当△DCE旋转至点A,D,E在同一直线上,连接BE,易证△BCE≌△ACD.则
①∠BEC=°;②线段AD、BE之间的数量关系是 .
(2)拓展研究:
如图2,△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=90°,点A、D、E在同一直线上,若AE=15,DE=7,求AB的长度.
(3)探究发现:
如图3,P为等边△ABC内一点,且∠APC=150°,且∠APD=30°,AP=5,CP=4,DP=8,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
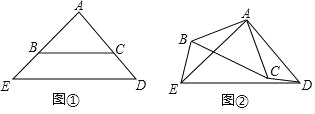
【题目】(1)问题发现
如图①,△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,点B在线段AE上,点C在线段AD上,请直接写出线段BE与线段CD的数量关系: ;
(2)操作探究
如图②,将图①中的△ABC绕点A顺时针旋转,旋转角为α(0<α<360),请判断线段BE与线段CD的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点O为Rt△ABC斜边AC上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE. 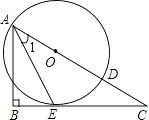
(1)求证:AE平分∠CAB;
(2)探求图中∠1与∠C的数量关系,并求当AE=EC时tanC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,CO⊥AB于点O,CD是⊙O的切线,切点为D.连接BD,交OC于点E. 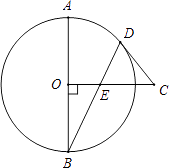
(1)求证:∠CDE=∠CED;
(2)若AB=13,BD=12,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com