
【题目】综合题。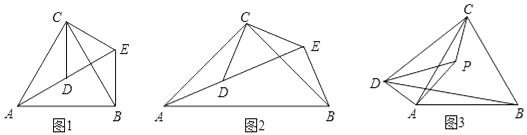
(1)问题发现:如图1,△ACB和△DCE均为等边三角形,当△DCE旋转至点A,D,E在同一直线上,连接BE,易证△BCE≌△ACD.则
①∠BEC=°;②线段AD、BE之间的数量关系是 .
(2)拓展研究:
如图2,△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=90°,点A、D、E在同一直线上,若AE=15,DE=7,求AB的长度.
(3)探究发现:
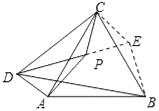
如图3,P为等边△ABC内一点,且∠APC=150°,且∠APD=30°,AP=5,CP=4,DP=8,求BD的长.
【答案】
(1)120;AD=BE
(2)
解:∵△ACB和△DCE均为等腰直角三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=90°.
∴∠ACD=∠BCE.
在△ACD和△BCE中, 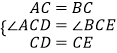 ,
,
∴△ACD≌△BCE(SAS).
∴AD=BE=AE﹣DE=15﹣7=8,∠ADC=∠BEC,
∵△DCE为等腰直角三角形
∴∠CDE=∠CED=45°.
∵点A,D,E在同一直线上,
∴∠ADC=135°.
∴∠BEC=135°.
∴∠AEB=∠BEC﹣∠CED=90°.
∴AB= ![]() =
= ![]() =17
=17
(3)
解:把△APC绕点C逆时针旋转60°得△BEC,连接PE,如图所示:
则△BEC≌△APC,
∴CE=CP,∠PCE=60°,BE=AP=5,∠BEC=∠APC=150°,
∴△PCE是等边三角形,
∴∠EPC=∠PEC=60°,PE=CP=4,
∴∠BED=∠BEC﹣∠PEC=90°,
∵∠APD=30°,
∴∠DPC=150°﹣30°=120°,
又∵∠DPE=∠DPC+∠EPC=120°+60°=180°,
即D、P、E在同一条直线上,
∴DE=DP+PE=8+4=12,
在Rt△BDE中, ![]() ,
,
即BD的长为13.
【解析】解:(1)①∵△ACB和△DCE均为等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°.
∴∠ACD=∠BCE.
在△ACD和△BCE中, 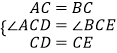 ,
,
∴△ACD≌△BCE(SAS).
∴∠ADC=∠BEC.
∵△DCE为等边三角形,
∴∠CDE=∠CED=60°.
∵点A,D,E在同一直线上,
∴∠ADC=120°.
∴∠BEC=120°.
故答案为:120.
②由①得:△ACD≌△BCE,
∴AD=BE;
故答案为:AD=BE.
(1)由条件易证△ACD≌△BCE,从而得到:AD=BE,∠ADC=∠BEC.由点A,D,E在同一直线上可求出∠ADC,从而可以求出∠BEC的度数.(2)同(1)证出△ACD≌△BCE,得出AD=BE=AE﹣DE=8,∠ADC=∠BEC,求出∠BEC=135°,得出∠AEB=∠BEC﹣∠CED=90°.由勾股定理求出AB即可;(3)把△APC绕点C逆时针旋转60°得△BEC,连接PE,则△BEC≌△APC,得出CE=CP,∠PCE=60°,BE=AP=5,∠BEC=∠APC=150°,证出△PCE是等边三角形,得出∠EPC=∠PEC=60°,PE=CP=4,求出∠BED=∠BEC﹣∠PEC=90°,证明D、P、E在同一条直线上,得出DE=DP+PE=12,再由勾股定理求出BD即可.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】 我们知道在同一平面内,两条平行直线的交点有0个,两条相交直线的交点有1个,平面内三条平行直线的交点有0个,经过同一点的三条直线的交点有1个……
(1)平面上有三条互不重合的直线,请画图探究它们的交点个数;
(2)若平面内的五条直线恰有4个交点,请画出符合条件的所有图形;
(3)在平面内画出10条直线,使它们的交点个数恰好是32.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师自驾轿车沿高速公路从A地到B地旅游,途经两座跨海大桥,共用了4.5小时;返回时平均速度提高了10千米/小时,比去时少用了半小时回到A地.
(1)求A、B两地间的路程.
(2)两座跨海大桥的长度及过桥费见表.

该省交通部门规定:轿车的高速公路通行费y(元)的计算方法为:y=ax+b+5,其中a(元/千米)为高速公路里程费,x(千米)为高速公路里程(不包括跨海大桥长),b(元)为跨海大桥过桥费.若王老师从A地到B地所花的高速公路通行费为295.4元,求轿车的高速公路里程费a.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆客车从甲地开往乙地,一辆轿车从乙地开往甲地,两车同时出发,两车行驶x小时后,记客车离甲地的距离为y1千米,轿车离甲地的距离为y2千米,y1、y2关于x的函数图象如图.
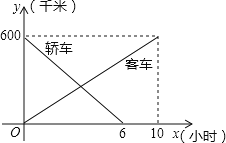
(1)根据图象,直接写出y1、y2关于x的函数关系式;
(2)当两车相遇时,求此时客车行驶的时间;
(3)两车相距200千米时,求客车行驶的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究归纳题:
![]()
(1)试验
如图1,直线上有两点A与B,图中有线段___条;
(2)拓展延伸:
图2直线上有A,B,C三个点,以A为端点,有线段AB,线段AC;同样以C为端点,有线段CA,线段CB;以B为端点,有线段BA,线段BC,去除重复线段,图2共有___条线段;
同样方法探究出图3中有_____条线段;
(3)探索归纳:
如果直线上有n(n为正整数)个点,则共有________条线段.(用含n的式子表示)
(4)解决问题:
①中职篮(CBA)2018——2019赛季,比赛队伍数仍然为20支,截止2018年12月14日,赛程已经过半(每两队之间都赛了一场),请你帮助计算一下目前一共进行了多少场比赛?
②2018年11月30日,赤峰至京沈高铁喀左站客运专线路基工程全部完成,将正式进入轨道铺设阶段,预计2020年7月1日通车,北京至赤峰有北京星火站,顺义西站,怀柔南站,密云站,兴隆西站,安匠站,承德南站,承德县北站,平泉北站,牛河梁站,喀左站,宁城站、平庄西站、赤峰西站等共计14个车站,请你帮助计算一下,应该设计多少种高铁车票?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践操作题 某班学生植树,若每人植7棵树,则剩5棵树;若每人植8棵树,则有1人少植1棵树,问有多少名学生植树,有多少棵树.
(1)假设有x名学生植树,有y棵树,请列出关于这个问题的二元一次方程组;
(2)用列表的方法求出有多少名学生植树,有多少棵树.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在等边三角形ABC中,
①如图①,D,E分别是边AC,AB上的点且AE=CD,BD与EC交于点F,则∠BFE的度数是 度;
②如图②,D,E分别是边AC,BA延长线上的点且AE=CD,BD与EC的延长线交于点F,此时∠BFE的度数是 度;
(2)如图③,在△ABC中,AC=BC,∠ACB是锐角,点O是AC边的垂直平分线与BC的交点,点D,E分别在AC,OA的延长线上,AE=CD,BD与EC的延长线交于点F,若∠ACB=α,求∠BFE的大小.(用含α的代数式表示).
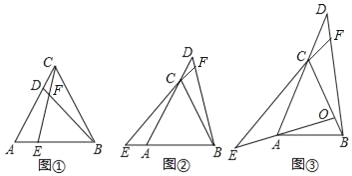
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上两点A,B对应的数分别为﹣4,8.
(1)如图1,如果点P和点Q分别从点A,B同时出发,沿数轴负方向运动,点P的运动速度为每秒2个单位,点Q的运动速度为每秒6个单位.
①A,B两点之间的距离为 .
②当P,Q两点相遇时,点P在数轴上对应的数是 .
③求点P出发多少秒后,与点Q之间相距4个单位长度?
(3)如图2,如果点P从点A出发沿数轴的正方向以每秒2个单位的速度运动,点Q从点B出发沿数轴的负方向以每秒6个单位的速度运动,点M从数轴原点O出发沿数轴的正方向以每秒1个单位的速度运动,若三个点同时出发,经过多少秒后有MP=MQ?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com