
【题目】实践操作题 某班学生植树,若每人植7棵树,则剩5棵树;若每人植8棵树,则有1人少植1棵树,问有多少名学生植树,有多少棵树.
(1)假设有x名学生植树,有y棵树,请列出关于这个问题的二元一次方程组;
(2)用列表的方法求出有多少名学生植树,有多少棵树.
科目:初中数学 来源: 题型:
【题目】如图,点A(1,3)、点B(m,1)是一次函数![]() 的图像上的两点,一次函数
的图像上的两点,一次函数![]() 图像与x轴交于点D.
图像与x轴交于点D.

(1)b = ,m = ;
(2)过点B作直线l垂直于x轴,点E是点D关于直线l的对称点,点C是点A关于原点的对称点.试判断点B、E、C是否在同一条直线上,并说明理由.
(3)连结AO、BO,求△AOB的面积;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中有3个分别标有数字﹣1、1、2的小球,它们除标的数字不同外无其他区别.
(1)随机地从口袋中取出一小球,求取出的小球上标的数字为负数的概率;
(2)随机地从口袋中取出一小球,放回后再取出第二个小球,求两次取出的数字的和等于0的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题。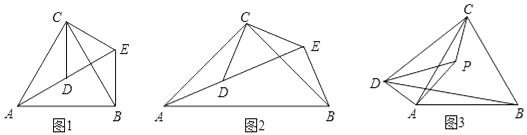
(1)问题发现:如图1,△ACB和△DCE均为等边三角形,当△DCE旋转至点A,D,E在同一直线上,连接BE,易证△BCE≌△ACD.则
①∠BEC=°;②线段AD、BE之间的数量关系是 .
(2)拓展研究:
如图2,△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=90°,点A、D、E在同一直线上,若AE=15,DE=7,求AB的长度.
(3)探究发现:
如图3,P为等边△ABC内一点,且∠APC=150°,且∠APD=30°,AP=5,CP=4,DP=8,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图①,△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,点B在线段AE上,点C在线段AD上,请直接写出线段BE与线段CD的数量关系: ;
(2)操作探究
如图②,将图①中的△ABC绕点A顺时针旋转,旋转角为α(0<α<360),请判断线段BE与线段CD的数量关系,并说明理由.
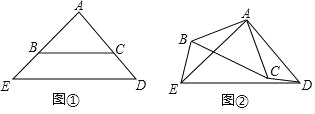
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为直线x=1,有如下结论:
①c<1;
②2a+b=0;
③b2<4ac;
④若方程ax2+bx+c=0的两根为x1 , x2 , 则x1+x2=2.
则正确的结论是( )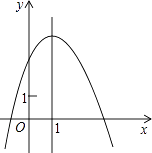
A.①②
B.①③
C.②④
D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是等边三角形,在直线AC、直线BC上分别取点D和点且AD=CE,直线BD、AE相交于点F.
(1)如图1所示,当点D、点E分别在线段CA、BC上时,求证:BD=AE;
(2)如图2所示,当点D、点E分别在CA、BC的延长线时,求∠BFE的度数;
(3)如图3所示,在(2)的条件下,过点C作CM∥BD,交EF于点M,若DF:AF:AM=1:2:4,BC=12,求CE的长度.
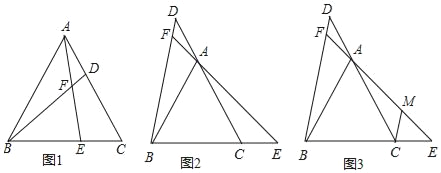
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列一元一次方程解应用题:
某管道由甲、乙两工程队单独施工分别需要30天、20天.
(1)如果两队从管道两端同时施工,需要多少天完工?
(2)又知甲队单独施工每天需付200元施工费,乙队单独施工每天需付280元施工费,那么是由甲队单独施工,还是由乙队单独施工,还是由两队同时施工?请你按照少花钱多办事的原则,设计一个方案,并通过计算说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com