
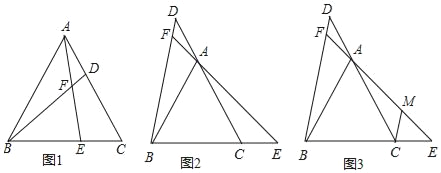
【题目】已知△ABC是等边三角形,在直线AC、直线BC上分别取点D和点且AD=CE,直线BD、AE相交于点F.
(1)如图1所示,当点D、点E分别在线段CA、BC上时,求证:BD=AE;
(2)如图2所示,当点D、点E分别在CA、BC的延长线时,求∠BFE的度数;
(3)如图3所示,在(2)的条件下,过点C作CM∥BD,交EF于点M,若DF:AF:AM=1:2:4,BC=12,求CE的长度.
【答案】(1)证明见解析;(2)60°;(3)6.
【解析】
(1)先判断出∠BAC=∠ACB,进而用SAS即可判断出△ABD≌△CAE,即可得出结论;
(2)先判断出∠BAD=∠ACE=120°,进而用SAS即可判断出△ABD≌△CAE,即可得出结论;
(3)先求出AC=12,再判断出△ADF∽△ACM,即可得出结论.
解:(1)∵△ABC是等边三角形,
∴∠BAC=∠ACB=60°,AB=AC,
在△ABD和△CAE中,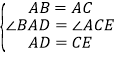 ,
,
∴△ABD≌△CAE,
∴BD=AE,
(2)∵△ABC是等边三角形,
∴∠BAC=∠ACB=60°,AB=AC,
∴∠BAD=∠ACE=120°
在△ABD和△CAE中,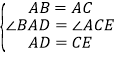 ,
,
∴△ABD≌△CAE,
∴∠ADB=∠CEA,
∴∠BFE=∠ADB+∠DAF=∠AEC+∠CAE=∠ACB=60°;
(3)∵CM∥BD,
∴△ADF∽△ACM,
∴![]() ,
,
∵AF:AM=2:4=1:2,
∴AD=![]() AC,
AC,
∵△ABC是等边三角形,
∴AC=BC=12,
∴AD=6,
∵AD=CE,
∴CE=AD=6.


科目:初中数学 来源: 题型:
【题目】王老师自驾轿车沿高速公路从A地到B地旅游,途经两座跨海大桥,共用了4.5小时;返回时平均速度提高了10千米/小时,比去时少用了半小时回到A地.
(1)求A、B两地间的路程.
(2)两座跨海大桥的长度及过桥费见表.

该省交通部门规定:轿车的高速公路通行费y(元)的计算方法为:y=ax+b+5,其中a(元/千米)为高速公路里程费,x(千米)为高速公路里程(不包括跨海大桥长),b(元)为跨海大桥过桥费.若王老师从A地到B地所花的高速公路通行费为295.4元,求轿车的高速公路里程费a.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践操作题 某班学生植树,若每人植7棵树,则剩5棵树;若每人植8棵树,则有1人少植1棵树,问有多少名学生植树,有多少棵树.
(1)假设有x名学生植树,有y棵树,请列出关于这个问题的二元一次方程组;
(2)用列表的方法求出有多少名学生植树,有多少棵树.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在等边三角形ABC中,
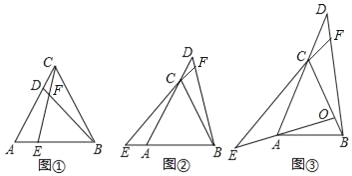
①如图①,D,E分别是边AC,AB上的点且AE=CD,BD与EC交于点F,则∠BFE的度数是 度;
②如图②,D,E分别是边AC,BA延长线上的点且AE=CD,BD与EC的延长线交于点F,此时∠BFE的度数是 度;
(2)如图③,在△ABC中,AC=BC,∠ACB是锐角,点O是AC边的垂直平分线与BC的交点,点D,E分别在AC,OA的延长线上,AE=CD,BD与EC的延长线交于点F,若∠ACB=α,求∠BFE的大小.(用含α的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一工地计划租用甲、乙两辆车清理淤泥,从运输量来估算:若租两辆车合运,10天可以完成任务;若单独租用乙车完成任务则比单独租用甲车完成任务多用15天.
(1)甲、乙两车单独完成任务分别需要多少天?
(2)已知两车合运共需租金65000元,甲车每天的租金比乙车每天的租金多1500元.试问:租甲乙车两车、单独租甲车、单独租乙车这三种方案中,哪一种租金最少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,过点A的双曲线y= ![]() 的一支在第一象限交梯形对角线OC于点D,交边BC于点E.
的一支在第一象限交梯形对角线OC于点D,交边BC于点E.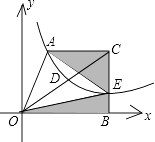
(1)填空:双曲线的另一支在第象限,k的取值范围是;
(2)若点C的坐标为(2,2),当点E在什么位置时,阴影部分的面积S最小?
(3)若 ![]() =
= ![]() ,S△OAC=2,求双曲线的解析式.
,S△OAC=2,求双曲线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABE,△BCD均为等边三角形,点A,B,C在同一条直线上,连接AD,EC,AD与EB相交于点M,BD与EC相交于点N,下列说法正确的有:___________
①AD=EC;②BM=BN;③MN∥AC;④EM=MB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上两点A,B对应的数分别为﹣4,8.
(1)如图1,如果点P和点Q分别从点A,B同时出发,沿数轴负方向运动,点P的运动速度为每秒2个单位,点Q的运动速度为每秒6个单位.
①A,B两点之间的距离为 .
②当P,Q两点相遇时,点P在数轴上对应的数是 .
③求点P出发多少秒后,与点Q之间相距4个单位长度?
(3)如图2,如果点P从点A出发沿数轴的正方向以每秒2个单位的速度运动,点Q从点B出发沿数轴的负方向以每秒6个单位的速度运动,点M从数轴原点O出发沿数轴的正方向以每秒1个单位的速度运动,若三个点同时出发,经过多少秒后有MP=MQ?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com