
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为直线x=1,有如下结论:
①c<1;
②2a+b=0;
③b2<4ac;
④若方程ax2+bx+c=0的两根为x1 , x2 , 则x1+x2=2.
则正确的结论是( )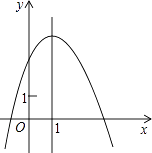
A.①②
B.①③
C.②④
D.③④
【答案】C
【解析】解:由抛物线与y轴的交点位置得到:c>1,选项①错误;
∵抛物线的对称轴为x=﹣ ![]() =1,∴2a+b=0,选项②正确;
=1,∴2a+b=0,选项②正确;
由抛物线与x轴有两个交点,得到b2﹣4ac>0,即b2>4ac,选项③错误;
令抛物线解析式中y=0,得到ax2+bx+c=0,
∵方程的两根为x1 , x2 , 且﹣ ![]() =1,及﹣
=1,及﹣ ![]() =2,
=2,
∴x1+x2=﹣ ![]() =2,选项④正确,
=2,选项④正确,
综上,正确的结论有②④.
故选C
由抛物线与y轴的交点在1的上方,得到c大于1,故选项①错误;由抛物线的对称轴为x=1,利用对称轴公式得到关于a与b的关系,整理得到2a+b=0,选项②正确;由抛物线与x轴的交点有两个,得到根的判别式大于0,整理可判断出选项③错误;令抛物线解析式中y=0,得到关于x的一元二次方程,利用根与系数的关系表示出两根之和,将得到的a与b的关系式代入可得出两根之和为2,选项④正确,即可得到正确的选项.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知:在Rt△ABC中,∠C=90°,sinA、sinB是方程x2+px+q=0的两个根.
(1)求实数p、q应满足的条件
(2)若p、q满足(1)的条件,方程x2+px+q=0的两个根是否等于Rt△ABC中两锐角A、B的正弦?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究归纳题:
![]()
(1)试验
如图1,直线上有两点A与B,图中有线段___条;
(2)拓展延伸:
图2直线上有A,B,C三个点,以A为端点,有线段AB,线段AC;同样以C为端点,有线段CA,线段CB;以B为端点,有线段BA,线段BC,去除重复线段,图2共有___条线段;
同样方法探究出图3中有_____条线段;
(3)探索归纳:
如果直线上有n(n为正整数)个点,则共有________条线段.(用含n的式子表示)
(4)解决问题:
①中职篮(CBA)2018——2019赛季,比赛队伍数仍然为20支,截止2018年12月14日,赛程已经过半(每两队之间都赛了一场),请你帮助计算一下目前一共进行了多少场比赛?
②2018年11月30日,赤峰至京沈高铁喀左站客运专线路基工程全部完成,将正式进入轨道铺设阶段,预计2020年7月1日通车,北京至赤峰有北京星火站,顺义西站,怀柔南站,密云站,兴隆西站,安匠站,承德南站,承德县北站,平泉北站,牛河梁站,喀左站,宁城站、平庄西站、赤峰西站等共计14个车站,请你帮助计算一下,应该设计多少种高铁车票?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践操作题 某班学生植树,若每人植7棵树,则剩5棵树;若每人植8棵树,则有1人少植1棵树,问有多少名学生植树,有多少棵树.
(1)假设有x名学生植树,有y棵树,请列出关于这个问题的二元一次方程组;
(2)用列表的方法求出有多少名学生植树,有多少棵树.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB:BC=3:4,AC=5,点P从点A出发,以每秒1个单位的速度,沿△ABC边A→B→C→A的方向运动,运动时间为t秒.
(1)求AB与BC的长;
(2)在点P的运动过程中,是否存在这样的点P,使△CDP为等腰三角形?若存在,求出t值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在等边三角形ABC中,
①如图①,D,E分别是边AC,AB上的点且AE=CD,BD与EC交于点F,则∠BFE的度数是 度;
②如图②,D,E分别是边AC,BA延长线上的点且AE=CD,BD与EC的延长线交于点F,此时∠BFE的度数是 度;
(2)如图③,在△ABC中,AC=BC,∠ACB是锐角,点O是AC边的垂直平分线与BC的交点,点D,E分别在AC,OA的延长线上,AE=CD,BD与EC的延长线交于点F,若∠ACB=α,求∠BFE的大小.(用含α的代数式表示).
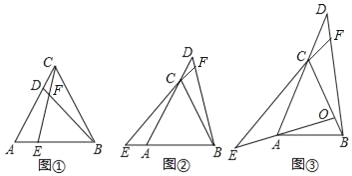
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一工地计划租用甲、乙两辆车清理淤泥,从运输量来估算:若租两辆车合运,10天可以完成任务;若单独租用乙车完成任务则比单独租用甲车完成任务多用15天.
(1)甲、乙两车单独完成任务分别需要多少天?
(2)已知两车合运共需租金65000元,甲车每天的租金比乙车每天的租金多1500元.试问:租甲乙车两车、单独租甲车、单独租乙车这三种方案中,哪一种租金最少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABE,△BCD均为等边三角形,点A,B,C在同一条直线上,连接AD,EC,AD与EB相交于点M,BD与EC相交于点N,下列说法正确的有:___________
①AD=EC;②BM=BN;③MN∥AC;④EM=MB.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com