
【题目】已知:在Rt△ABC中,∠C=90°,sinA、sinB是方程x2+px+q=0的两个根.
(1)求实数p、q应满足的条件
(2)若p、q满足(1)的条件,方程x2+px+q=0的两个根是否等于Rt△ABC中两锐角A、B的正弦?
【答案】
(1)
解:∵sinA、sinB是方程x2+px+q=0的两个根,∴sinA+sinB=﹣p,即:sinA+cosA=﹣p,∴![]() sin(A+45°)=﹣p
sin(A+45°)=﹣p
∵0°<A<90°,∴1<﹣p≤![]() ,∴﹣
,∴﹣![]() ≤p<﹣1,∵sinAsinB=q,即sinAcosA=q,∴sin2A=2q,∴0<q<
≤p<﹣1,∵sinAsinB=q,即sinAcosA=q,∴sin2A=2q,∴0<q<![]() ,
,
∵sin2A+sinB2=(sinA+sinB)2﹣2sinAsinB,∴p2﹣2q=1,
∴实数p、q应满足的条件是:p2﹣2q=1,∴﹣![]() ≤p<﹣1,0<q≤
≤p<﹣1,0<q≤![]() .
.
(2)
解:∵0<q≤![]() ,设sin2A=2q,则2A=2a,或180°﹣2a,即:A=a或90°﹣a,
,设sin2A=2q,则2A=2a,或180°﹣2a,即:A=a或90°﹣a,
∵sina和sin(90°﹣a)是方程的两根,即它们是直角三角形的两个锐角的正弦值.
【解析】(1)根据sinA+cosA=![]() sin(A+45°),sinAcosA=
sin(A+45°),sinAcosA=![]() sin2A,以及根与系数的关系,即可得到关于p,q的不等式,以及sin2A+sinB2=1,即可求得p,q的关系.
sin2A,以及根与系数的关系,即可得到关于p,q的不等式,以及sin2A+sinB2=1,即可求得p,q的关系.
(2)根据(1)可以得到sin2A=2q,求得A的值,证明A的值可以取互余的两个角的度数,即可证得.
【考点精析】认真审题,首先需要了解锐角三角函数的增减性(当角度在0°~90°之间变化时:(1)正弦值随着角度的增大(或减小)而增大(或减小)(2)余弦值随着角度的增大(或减小)而减小(或增大)(3)正切值随着角度的增大(或减小)而增大(或减小)(4)余切值随着角度的增大(或减小)而减小(或增大)).


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】在(1)![]() (2)
(2) ![]() (3)
(3) ![]() (4)
(4) ![]() 中,________是方程7x-3y=2的解;________是方程2x+y=8的解;________是方程组
中,________是方程7x-3y=2的解;________是方程2x+y=8的解;________是方程组![]() 的解.(填序号)
的解.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,西安路与南京路平行,并且与八一街垂直,曙光路与环城路垂直.如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走,最近的路程约为( )
A.600m
B.500m
C.400m
D.300m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(1,3)、点B(m,1)是一次函数![]() 的图像上的两点,一次函数
的图像上的两点,一次函数![]() 图像与x轴交于点D.
图像与x轴交于点D.

(1)b = ,m = ;
(2)过点B作直线l垂直于x轴,点E是点D关于直线l的对称点,点C是点A关于原点的对称点.试判断点B、E、C是否在同一条直线上,并说明理由.
(3)连结AO、BO,求△AOB的面积;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有16个只有颜色不同的球,其中红球有x个,白球有2x个,其他均为黄球,现甲从布袋中随机摸出一个球,若是红球则甲同学获胜,甲同学把摸出的球放回并搅匀,由乙同学随机摸出一个球,若为黄球,则乙同学获胜。
(1)当X=3时,谁获胜的可能性大?
(2)当x为何值时,游戏对双方是公平的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面四个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④AP垂直平分RS.其中正确结论的序号是 (请将所有正确结论的序号都填上).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中有3个分别标有数字﹣1、1、2的小球,它们除标的数字不同外无其他区别.
(1)随机地从口袋中取出一小球,求取出的小球上标的数字为负数的概率;
(2)随机地从口袋中取出一小球,放回后再取出第二个小球,求两次取出的数字的和等于0的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为直线x=1,有如下结论:
①c<1;
②2a+b=0;
③b2<4ac;
④若方程ax2+bx+c=0的两根为x1 , x2 , 则x1+x2=2.
则正确的结论是( )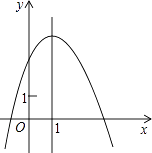
A.①②
B.①③
C.②④
D.③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com