
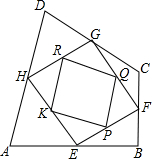
 如图,ABCD是校内一块四边形空地,学校在征集对这块空地种花草的设计中选定了如下方案:把这块四边形空地分成九块,种植三种不同品种的花草,其中E,F,G,H分别是AB,BC,CD,DA的中点,P,Q,R,K分别是EF,FG,GH,HE的中点,现在要在四边形PQRK中种上红色的花,在△PFQ,△QGR,△RHK,△KEP中种上黄色的花,在△HAE,△EBF,△FCG,△GDH中种上紫色的花.已知红,黄,紫三种花的单价分别是8元/m2,10元/m2,12元/m2,而种红花共用去120元,请用学过的数学知识计算种满四边形ABCD这块空地的花需要多少元?
如图,ABCD是校内一块四边形空地,学校在征集对这块空地种花草的设计中选定了如下方案:把这块四边形空地分成九块,种植三种不同品种的花草,其中E,F,G,H分别是AB,BC,CD,DA的中点,P,Q,R,K分别是EF,FG,GH,HE的中点,现在要在四边形PQRK中种上红色的花,在△PFQ,△QGR,△RHK,△KEP中种上黄色的花,在△HAE,△EBF,△FCG,△GDH中种上紫色的花.已知红,黄,紫三种花的单价分别是8元/m2,10元/m2,12元/m2,而种红花共用去120元,请用学过的数学知识计算种满四边形ABCD这块空地的花需要多少元? 分析 此题上实际上求种植每一种花的面积,利用面积×单价=总价来求每一种花所需的费用即可.利用三角形中位线定理和相似多边形的性质来求其面积.
解答  解:∵红花的单价分别是8元/m2,种红花共用去120元,
解:∵红花的单价分别是8元/m2,种红花共用去120元,
∴种红花的面积为:$\frac{120}{8}$=15(m2),
即S四边形PQRK=15m2.
如图,连接AC、BD.
∵点H、G分别是AD、CD的中点,
∴HG是△ADC的中位线,
∴HG∥AC,且HG=$\frac{1}{2}$AC,
∴△DHG∽△DAC,
∴$\frac{{S}_{△DHG}}{{S}_{△DAC}}$=($\frac{HG}{AC}$)2=$\frac{1}{4}$.
∴S△DHG=$\frac{1}{4}$S△DAC.
同理,S△AHE=$\frac{1}{4}$S△ABD,S△BEF=$\frac{1}{4}$S△ABC,S△CGF=$\frac{1}{4}$S△CDB,
∴S△DHG+S△AHE+S△BEF+S△CGF=$\frac{1}{4}$(S△DAC+S△ABD+S△ABC+S△CDB)=$\frac{1}{2}$S四边形ABCD.
∴S四边形HEFG=$\frac{1}{2}$S四边形ABCD.
同理,S四边形PQRK=$\frac{1}{2}$S四边形HEFG=$\frac{1}{4}$S四边形ABCD=15m2,
∴S四边形ABCD=60m2,S四边形HEFG=30m2,
∴种黄花的面积为:S四边形HEFG-S四边形PQRK=15m2.
种紫花的面积为:$\frac{1}{2}$S四边形ABCD=30m2.
则总费用为:120+15×10+30×12=630(元).
答:种满四边形ABCD这块空地的花需要720元.
点评 本题考查了中点四边形.要求学生灵活运用三角形的中位线定理,相似三角形的判定与性质,是一道综合题.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com