
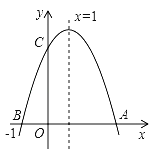
【题目】如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则①二次函数的最大值为a+b+c;②a﹣b+c<0;③b2﹣4ac<0;④当y>0时,﹣1<x<3,其中结论正确的有( )
A.①③B.①④C.①②D.①③④
【答案】B
【解析】
由图象可知,当x=1时,y=a+b+c最大,故①正确;当x=﹣1时,y=a﹣b+c=0,故②错误;二次函数与x轴有两个不同交点,因此b2﹣4ac>0,故③错误;对称轴为x=1,B(﹣1,0),所以A(3,0),由图象可得,y>0时,﹣l<x<3,故④正确.
解:①由图象可知,x=1时,y=a+b+c最大,因此二次函数的最大值为a+b+c,故①正确;
②由图象可知,x=-1时,y=0,即a-b+c=0,因此a-b+c=0,故②错误;
③由图象可知,函数图象与x轴有两个不同交点,因此b2﹣4ac>0,故③错误;
④∵对称轴为x=1,B(-1,0),
∴A(3,0),
∴y>0时,-1<x<3,
故④正确,
则答案为:①④.
故选:B.


科目:初中数学 来源: 题型:
【题目】在研究相似问题时,甲、乙同学的观点如下:
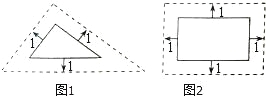
甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形相似.
对于两人的观点,下列说法正确的是( )
A.甲对,乙不对 B.甲不对,乙对 C.两人都对 D.两人都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 为坐标原点,点
为坐标原点,点![]() 是反比例函数
是反比例函数![]() 上的点,过点
上的点,过点![]() 作直线
作直线![]() ,直线
,直线![]() 交
交![]() 轴的正半轴于点
轴的正半轴于点![]() ,点
,点![]() 的坐标为
的坐标为![]() .设三角形
.设三角形![]() 的面积为
的面积为![]() ,且
,且![]() .
.
(1)当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(2)若![]() ,求反比例函数的解析式;
,求反比例函数的解析式;
(3)在(2)的结论下,设反比例函数上的一动点![]() ,
,![]() 是小于20的整数,求
是小于20的整数,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面内容:我们已经学习了《二次根式》和《乘法公式》,聪明的你可以发现:当![]() ,
,![]() 时,∵
时,∵![]() ,∴
,∴![]() ,当且仅当
,当且仅当![]() 时取等号.请利用上述结论解决以下问题:
时取等号.请利用上述结论解决以下问题:
(1)当![]() 时,
时,![]() 的最小值为_______;当
的最小值为_______;当![]() 时,
时,![]() 的最大值为__________.
的最大值为__________.
(2)当![]() 时,求
时,求![]() 的最小值.
的最小值.
(3)如图,四边形ABCD的对角线AC ,BD相交于点O,△AOB、△COD的面积分别为4和9,求四边形ABCD面积的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
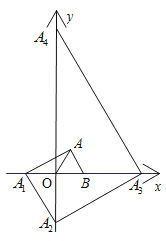
【题目】已知:如图,在平面直角坐标系中,点B的坐标为(1,0),以OB为边,在第一象限内作等边三角形OAB,过点A作AB的垂线,交x轴于点![]() ,过点
,过点![]() 作
作![]() 的垂线,交y轴于点
的垂线,交y轴于点![]() ,过点
,过点![]() 作
作![]() 的垂线,交x轴于点
的垂线,交x轴于点![]() ,过点
,过点![]() 作
作![]() 的垂线,交y轴于点
的垂线,交y轴于点![]() ,…,这样一直作下去,则点
,…,这样一直作下去,则点![]() 的坐标为______.
的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
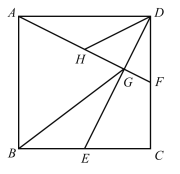
【题目】如图,在边长为4的正方形![]() 中,点
中,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,![]() 、
、![]() 交于点
交于点![]() ,
,![]() 的中点为
的中点为![]() ,连接
,连接![]() 、
、![]() .给出下列结论:①
.给出下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论有________.(请填上所有正确结论的序号)
.其中正确的结论有________.(请填上所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
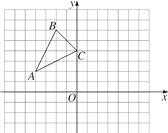
【题目】如图,已知A(-4,2),B(-2,6),C(0,4)是直角坐标系中的三点.
(1)把△ABC向右平移4个单位再向下平移1个单位,得到△A1B1C1,画出平移后的图形,并写出点A的对应点A1的坐标;
(2)以原点O为位似中心,将△ABC缩小为原来的一半,得到△A2B2C2,请在所给的坐标系中作出所有满足条件的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节是中国的传统节日.今年端午节前夕,遂宁市某食品厂抽样调查了河东某居民区市民对A、B、C、D四种不同口味粽子样品的喜爱情况,并将调查情况绘制成如图两幅不完整统计图:
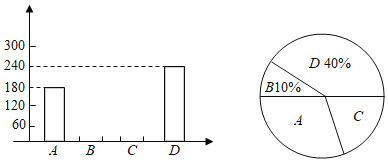
(1)本次参加抽样调查的居民有 人.
(2)喜欢C种口味粽子的人数所占圆心角为 度.根据题中信息补全条形统计图.
(3)若该居民小区有6000人,请你估计爱吃D种粽子的有 人.
(4)若有外型完全相同的A、B、C、D棕子各一个,煮熟后,小李吃了两个,请用列表或画树状图的方法求他第二个吃的粽子恰好是A种粽子的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com