
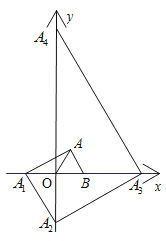
【题目】已知:如图,在平面直角坐标系中,点B的坐标为(1,0),以OB为边,在第一象限内作等边三角形OAB,过点A作AB的垂线,交x轴于点![]() ,过点
,过点![]() 作
作![]() 的垂线,交y轴于点
的垂线,交y轴于点![]() ,过点
,过点![]() 作
作![]() 的垂线,交x轴于点
的垂线,交x轴于点![]() ,过点
,过点![]() 作
作![]() 的垂线,交y轴于点
的垂线,交y轴于点![]() ,…,这样一直作下去,则点
,…,这样一直作下去,则点![]() 的坐标为______.
的坐标为______.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】随着互联网的高速发展,人们的支付方式发生了巨大改变,某学习小组抽样调查了春节期间某商场顾客的支付方式,主要有现金支付、银联卡支付和手机支付,调查得知使用这三种支付的人数比为![]() ,手机支付已成为市民购物便捷支付方式.手机支付主要有以下三种方式:
,手机支付已成为市民购物便捷支付方式.手机支付主要有以下三种方式:![]() ~支付宝,
~支付宝,![]() ~微信,
~微信,![]() ~其他.现将使用手机支付方式人数的调查结果绘制成如下不完整的统计图.
~其他.现将使用手机支付方式人数的调查结果绘制成如下不完整的统计图.

(1)扇形统计图中,![]() ________;请补全条形统计图;
________;请补全条形统计图;
(2)若该商场春节期间共20000人购物,请估计用支付宝进行支付的人数.
(3)经调查某天顾客现金支付、银联卡支付、手机支付每笔交易发生的平均金额分别为120元、260元、80元,求这天顾客每笔交易的平均金额.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过
经过![]() ,
,![]() 两点,与x轴的另一个交点为C,顶点为D,连结CD.
两点,与x轴的另一个交点为C,顶点为D,连结CD.
(1)求该抛物线的表达式;
(2)点P为该抛物线上一动点(与点B、C不重合),设点P的横坐标为t.
①当点P在直线BC的下方运动时,求![]() 的面积的最大值;
的面积的最大值;
②该抛物线上是否存在点P,使得![]() 若存在,求出所有点P的坐标;若不存在,请说明理由.
若存在,求出所有点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则①二次函数的最大值为a+b+c;②a﹣b+c<0;③b2﹣4ac<0;④当y>0时,﹣1<x<3,其中结论正确的有( )
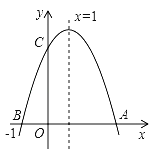
A.①③B.①④C.①②D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
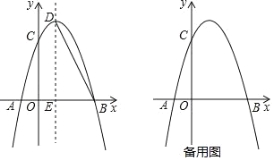
【题目】如图,抛物线y=-![]() x2+bx+c与x轴交于A、B两点,与y轴交于点C,点B坐标为(4,0),点C坐标为(0,4),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
x2+bx+c与x轴交于A、B两点,与y轴交于点C,点B坐标为(4,0),点C坐标为(0,4),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
(1)求抛物线的表达式及对称轴;
(2)点F是抛物线上的动点,当∠FBA=2∠BDE时,求点F的坐标;
(3)若点P是x轴上方抛物线上的动点,以PB为边作正方形PBGH,随着点P的运动,正方形的大小、位置也随着改变,当顶点G或H恰好落在y轴上时,请直接写出点P的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司招聘人才,对应聘者分别进行阅读能力、思维能力和表达能力三项测试,其中甲、乙两人的成绩如下表(单位:分):
项目人员 | 阅读能力 | 思维能力 | 表达能力 |
甲 | 93 | 86 | 73 |
乙 | 95 | 81 | 79 |
(1)根据实际需要,公司将阅读、思维和表达能力三项测试得分按3:5:2的比确定每人的最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
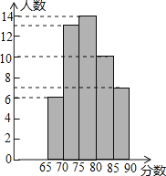
(2)公司按照(1)中的成绩计算方法,将每位应聘者的最后成绩绘制成如图所示的频数分布直方图(每组分数段均包含左端数值,不包含右端数值,如最右边一组分数x为:85≤x<90),并决定由高分到低分录用8名员工,甲、乙两人能否被录用?请说明理由,并求出本次招聘人才的录用率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是用黑色棋子摆成的美丽图案,按照这样的规律摆下去,第10个这样的图案需要黑色棋子的个数为( )

![]()


A.148B.152C.174D.202
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com