
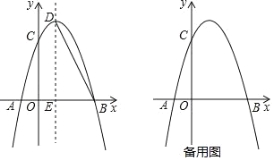
����Ŀ����ͼ��������y=-![]() x2+bx+c��x�ύ��A��B���㣬��y�ύ�ڵ�C����B����Ϊ(4��0)����C����Ϊ(0��4)����D�������ߵĶ��㣬����D��x��Ĵ��ߣ�����ΪE������BD��
x2+bx+c��x�ύ��A��B���㣬��y�ύ�ڵ�C����B����Ϊ(4��0)����C����Ϊ(0��4)����D�������ߵĶ��㣬����D��x��Ĵ��ߣ�����ΪE������BD��
��1���������ߵı���ʽ���Գ��
��2����F���������ϵĶ��㣬����FBA��2��BDEʱ�����F�����ꣻ
��3������P��x���Ϸ��������ϵĶ��㣬��PBΪ����������PBGH�����ŵ�P���˶��������εĴ�С��λ��Ҳ���Ÿı䣬������G��Hǡ������y����ʱ����ֱ��д����P�ĺ����꣮
���𰸡���1��![]() ��x=1����2��(
��x=1����2��(![]() ��
��![]() )��(
)��(![]() ��-
��-![]() )����3����P�ĺ�����Ϊ
)����3����P�ĺ�����Ϊ![]() ��0��2��2-
��0��2��2-![]()
��������
��1������B��C��������������߱���ʽ��������⣻
��2�����߶�DE��ȡ��M��ʹMD=MB����ʱ��EMB=2��BDE�����FBA=��EMB��������⣻
��3���ֵ�P�ڶԳ����Ҳࡢ��P�ڶԳ�������������������������ȫ����⼴�ɣ�
��1�����������
![]()
��![]()
![]()
��D�����꣨1��![]() �����Գ���Ϊx=1
�����Գ���Ϊx=1
��2����ͼ�����߶�DE��ѡȡ��M��ʹ��MD=MB����ʱ��EMB��2��BDE
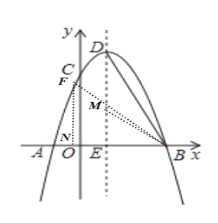
��ME=a����Rt��BME��ME2BE2BM2.
��![]() �����a��
�����a��![]()
��tan��EMB=![]()
��F��FN��x���ڵ�N����F��m����![]() m2+m+4������FN��|��
m2+m+4������FN��|��![]() m2+m+4|
m2+m+4|
�ߡ�FBA��2��BDE��
���FBA����EMB��
��tan��FBA=tan��EMB=![]()
��B��4��0����E��1��0����
��BE��3��BN��4/span>��m����tan��FBA=
����F��x���Ϸ�ʱ����12(4��m)��5����![]() m2+m+4�������m1��4(��)��m2��
m2+m+4�������m1��4(��)��m2��![]()
��F�����꣨![]() ��
��![]() ��
��
����F��x���·�ʱ����-12(4��m)��5����![]() m2+m+4�������m1��4(��)��m2��
m2+m+4�������m1��4(��)��m2��![]() ��F�����꣨
��F�����꣨![]() ��-
��-![]() ��
��
��F�����꣨![]() ��
��![]() ����
����![]() ��-
��-![]() ��
��
��3�����ٵ���P�ڶԳ����Ҳ�ʱ��
����������H��y����ʱ����ͼ2��
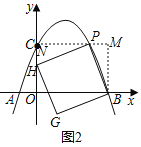
�ߡ�MPB+��CPH=90������CPH+��CHP=90����
���CHP=��MPB��
�ߡ�BMP=��PNH=90����PH=BP��
���BMP�ա�PNH��AAS����
��MB=PC��
���P��x��y������x=y=-![]() x2+x+4��
x2+x+4��
��ã�x=��2![]() ����ȥ��ֵ����
����ȥ��ֵ����
�ʵ�P�ĺ�����Ϊ2![]() ��
��
����������G��y����ʱ����ͼ3��
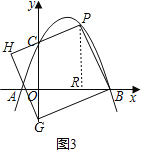
����P��PR��x���ڵ�R��
ͬ���ɵã���PRB�ա�BOG��AAS����
��PR=OB=4��
��yP=4=-![]() x2+x+4��
x2+x+4��
��ã�x=2��
�ڵ���P�ڶԳ������ʱ��
ͬ���ɵã���P�ĺ�����Ϊ0��2-2![]() ��
��
���ϣ���P�ĺ�����Ϊ![]() ��0��2��2-
��0��2��2-![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
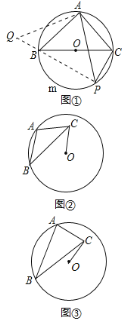
����Ŀ����1�����ⱳ������ͼ�٣�BC�ǡ�O��ֱ������A�ڡ�O�ϣ�AB��AC��PΪ![]() ��һ����(����B��C�غ�)����֤��
��һ����(����B��C�غ�)����֤��![]() PA��PB+PC���������ͼ�������������ߣ��������������֤�����̣�
PA��PB+PC���������ͼ�������������ߣ��������������֤�����̣�
��2�����Ǩ�ƣ���ͼ�ڣ���O�İ뾶Ϊ3����A��B�ڡ�O�ϣ�CΪ��O��һ�㣬AB��AC��AB��AC������ΪA����OC����Сֵ
��3����չ���죺��ͼ�ۣ���O�İ뾶Ϊ3����A��B�ڡ�O�ϣ�CΪ��O��һ�㣬AB��![]() AC��AB��AC������ΪA����OC����СֵΪ____________��
AC��AB��AC������ΪA����OC����СֵΪ____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
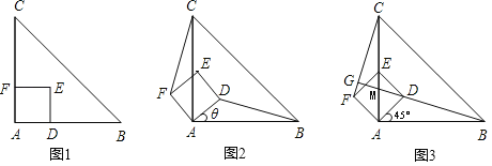
����Ŀ����ͼ1����ABC�ǵ���ֱ�������Σ��ı���ADEF�������Σ�D��F�ֱ���AB��AC���ϣ���ʱBD=CF��BD��CF������
��1����������ADEF�Ƶ�A��ʱ����ת����0��������90����ʱ����ͼ2��BD=CF����������������֤����������������˵�����ɣ�
��2����������ADEF�Ƶ�A��ʱ����ת45��ʱ����ͼ3���ӳ�BD��CF�ڵ�G, AC��BG�Ľ���ΪM����֤��EM:DM=CG:AC��
(3)��(2)С��������£���AB=4��AD=![]() ʱ�����ı���ABGF�������
ʱ�����ı���ABGF�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У�AC��BC��4����ACB��90����������BDEF�ı߳�Ϊ2����������BDEF�Ƶ�B��תһ�ܣ�����AE��BE��CD��
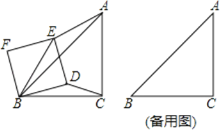
(1)���ҳ�ͼ������ABE���Ƶ������Σ���˵�����ɣ�
(2)����E���߶�AF��ʱCD�ij���
(3)��AE���е�ΪM������FM������FM����ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
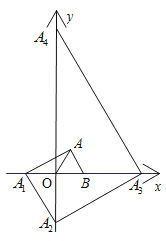
����Ŀ����֪����ͼ����ƽ��ֱ������ϵ�У���B������Ϊ(1��0)����OBΪ�ߣ��ڵ�һ���������ȱ�������OAB������A��AB�Ĵ��ߣ���x���ڵ�![]() ������
������![]() ��
��![]() �Ĵ��ߣ���y���ڵ�
�Ĵ��ߣ���y���ڵ�![]() ������
������![]() ��
��![]() �Ĵ��ߣ���x���ڵ�
�Ĵ��ߣ���x���ڵ�![]() ������
������![]() ��
��![]() �Ĵ��ߣ���y���ڵ�
�Ĵ��ߣ���y���ڵ�![]() ����������һֱ����ȥ�����
����������һֱ����ȥ�����![]() ������Ϊ______��
������Ϊ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������µ���������![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() �ǵ�һ�������������ϵ�һ�㣮
�ǵ�һ�������������ϵ�һ�㣮
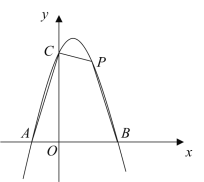
��1���������������Ӧ�ĺ�������ʽ��
��2�����ı���![]() �����Ϊ
�����Ϊ![]() ����
����![]() �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
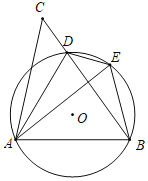
����Ŀ����ͼ��D����ABC��BC����һ�㣬����AD������ABD�����Բ������ADC��ֱ��AD�۵�����C�Ķ�Ӧ��E���ڡ�O�ϣ�
��1����֤��AE��AB��
��2����գ�
�ٵ���CAB��90����cos��ADB��![]() ��BE��2ʱ����BC�ij�Ϊ�� ����
��BE��2ʱ����BC�ij�Ϊ�� ����
�ڵ���BAE���� ��ʱ���ı���AOED�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() Ϊ
Ϊ![]() ��ֱ������
��ֱ������![]() ��
��![]() �Ҳ��Բ�ϵ�һ�����㣬��
�Ҳ��Բ�ϵ�һ�����㣬��![]() ��
��![]() ����Բ���е㣬
����Բ���е㣬![]() ��
��![]() �����ߣ��е�Ϊ
�����ߣ��е�Ϊ![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ����
Ϊ����![]() ��һ���㣬����
��һ���㣬����![]() ��
��![]()
![]() ��
��![]() ��
��
��1����![]() ʱ�� ��֤��
ʱ�� ��֤��![]() ��
��
��2����![]() �İ뾶Ϊ
�İ뾶Ϊ![]() ������գ�
������գ�
�����ı���![]() Ϊ������ʱ��
Ϊ������ʱ��![]()
����![]() ʱ�� �ı���
ʱ�� �ı���![]() Ϊ���Σ�
����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
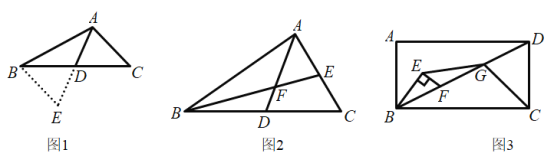
����Ŀ������̽����
С����������һ�����⣺��ͼ1��![]() �У�
��![]() ��
��![]() ��AD�����ߣ���AD��ȡֵ��Χ�����������ǣ��ӳ�AD��E��ʹ
��AD�����ߣ���AD��ȡֵ��Χ�����������ǣ��ӳ�AD��E��ʹ![]() ������BE��֤��
������BE��֤��![]() �����������ͼ���ʹ����õ������
�����������ͼ���ʹ����õ������
��ش𣺣�1��С��֤��![]() ���ж������ǣ�__________________________________________��
���ж������ǣ�__________________________________________��
��2��AD��ȡֵ��Χ��________________________��
�������ã�
��3����ͼ2��AD��![]() �����ߣ���AD��ȡһ��F������BF���ӳ���AC�ڵ�E��ʹ
�����ߣ���AD��ȡһ��F������BF���ӳ���AC�ڵ�E��ʹ![]() ����֤��
����֤��![]() ��
��
��4����ͼ3���ھ���ABCD�У�![]() ����BD��ȡһ��F����BFΪб����
����BD��ȡһ��F����BFΪб����![]() ����
����![]() ����G��DF���е㣬����EG��CG����֤��
����G��DF���е㣬����EG��CG����֤��![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com