
【题目】如图,在Rt△ABC中,AC=BC=4,∠ACB=90°,正方形BDEF的边长为2,将正方形BDEF绕点B旋转一周,连接AE、BE、CD.
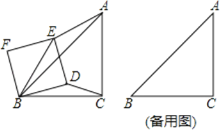
(1)请找出图中与△ABE相似的三角形,并说明理由;
(2)求当点E在线段AF上时CD的长;
(3)设AE的中点为M,连接FM,试求FM长的取值范围.
【答案】(1)证明见详解;(2)![]() ; (3)
; (3)![]() .
.
【解析】
(1)根据等腰三角形的性质和相似三角形的判定可以判断△ABE∽△CBD.
(2)根据相似三角形的性质得到AB=![]() BC=
BC=![]() ,根据勾股定理得AF=
,根据勾股定理得AF=![]() =
=![]() =
=![]() ,如图1,E在线段AF上,AE=AF-EF=
,如图1,E在线段AF上,AE=AF-EF=![]() ,从而求出CD的长.
,从而求出CD的长.
(3)如图2,延长EF到G,使FG=EF,连接AG,BG,求得△BFG是等腰直角三角形,得到BG=![]() BF=
BF=![]() ,设M为AE的中点,连接MF,根据三角形中位线定理得到AG=2FM,根据三角形的三边关系即可得出结论.
,设M为AE的中点,连接MF,根据三角形中位线定理得到AG=2FM,根据三角形的三边关系即可得出结论.
解:(1)△ABE∽△CBD,
∵在Rt△ABC中,AC=BC=4,∠ACB=90°,
∴∠ABC=∠EBD=45°,
∴∠ABE=∠CBD,
∵![]() =
=![]() ,
,![]() =
=![]() ,
,
∴![]() ,
,
∴△ABE∽△CBD;
(2)∵△ABE∽△CBD,
∴![]() =
=![]() =
=![]() ,
,
∴CD=![]() AE,
AE,
∵AC=BC=4,∠ACB=90°,
∴AB=![]() BC=
BC=![]() ,
,
∵当点E在线段AF上时CD的长,
∵∠AFB=90°,
∴AF=![]() =
=![]() =
=![]() ,
,
如图1,AE=AF﹣EF=![]() ﹣2,
﹣2,
∴CD=![]() ﹣
﹣![]() ;
;
所以CD的长为![]() ﹣
﹣![]() .
.
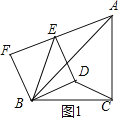
(3)如图2,延长EF到G使FG=EF,连接AG,BG,则△BFG是等腰直角三角形,
∴BG=![]() BF=
BF=![]() ,
,
设M为AE的中点,
连接MF,
∴MF是△AGE的中位线,
∴AG=2FM,
在△ABG中,∵AB﹣BG≤AG≤AB+BG,
∴![]() ≤AG≤
≤AG≤![]() ,
,
∴![]() ≤FM≤
≤FM≤![]() .
.
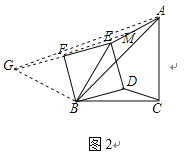


科目:初中数学 来源: 题型:
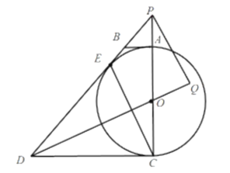
【题目】如图,在![]() 中,
中,![]() 是直径,
是直径,![]() 是切线,点
是切线,点![]() 为切点.
为切点.
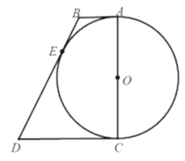
(1)求证:![]() ;
;
(2)如图,连接![]() 交于点
交于点![]() ,连接
,连接![]() 并延长,交
并延长,交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;

(3)如图,延长![]() 交于点
交于点![]() 连接
连接![]() 过点
过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .若
.若![]()
![]() 求
求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某百货公司进了一批商品,进货价为20元/件,有专家预计月销量![]() (件)关于售价
(件)关于售价![]() (元/件)的函数解析式为
(元/件)的函数解析式为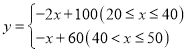
(1)若百货公司销售该商品月利润为![]() 元,写出
元,写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)当售价![]() 为多少时,百货公司销售该商品的月利润最大,最大月利润是多少?
为多少时,百货公司销售该商品的月利润最大,最大月利润是多少?
(3)当百货公司销售该商品的月利润不少于400元时,试确定商品的售价![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过
经过![]() ,
,![]() 两点,与x轴的另一个交点为C,顶点为D,连结CD.
两点,与x轴的另一个交点为C,顶点为D,连结CD.
(1)求该抛物线的表达式;
(2)点P为该抛物线上一动点(与点B、C不重合),设点P的横坐标为t.
①当点P在直线BC的下方运动时,求![]() 的面积的最大值;
的面积的最大值;
②该抛物线上是否存在点P,使得![]() 若存在,求出所有点P的坐标;若不存在,请说明理由.
若存在,求出所有点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
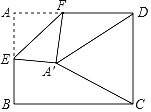
【题目】如图,在矩形纸片ABCD中,AB=4,BC=4![]() ,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A'EF,连接A'C,A'D,则当△A'DC是以A'D为腰的等腰三角形时,FD的长是_____.
,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A'EF,连接A'C,A'D,则当△A'DC是以A'D为腰的等腰三角形时,FD的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
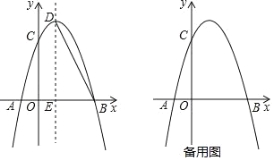
【题目】如图,抛物线y=-![]() x2+bx+c与x轴交于A、B两点,与y轴交于点C,点B坐标为(4,0),点C坐标为(0,4),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
x2+bx+c与x轴交于A、B两点,与y轴交于点C,点B坐标为(4,0),点C坐标为(0,4),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
(1)求抛物线的表达式及对称轴;
(2)点F是抛物线上的动点,当∠FBA=2∠BDE时,求点F的坐标;
(3)若点P是x轴上方抛物线上的动点,以PB为边作正方形PBGH,随着点P的运动,正方形的大小、位置也随着改变,当顶点G或H恰好落在y轴上时,请直接写出点P的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,且AM =![]() 海里,那么该船继续航行______海里可使渔船到达离灯塔距离最近的位置.
海里,那么该船继续航行______海里可使渔船到达离灯塔距离最近的位置.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新学期开始时,某校九年级一班的同学为了增添教室绿色文化,打造温馨舒适的学习环境,准备到一家植物种植基地购买A、B两种花苗.据了解,购买A种花苗3盆,B种花苗5盆,则需210元;购买A种花苗4盆,B种花苗10盆,则需380元.
(1)求A、B两种花苗的单价分别是多少元?
(2)经九年级一班班委会商定,决定购买A、B两种花苗共12盆进行搭配装扮教室.种植基地销售人员为了支持本次活动,为该班同学提供以下优惠:购买几盆B种花苗,B种花苗每盆就降价几元,请你为九年级一班的同学预算一下,本次购买至少准备多少钱?最多准备多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com