
【题目】如图,![]() 内接于
内接于![]() ,
,![]() ,
,![]() 为弧
为弧![]() 上一点,连
上一点,连![]()
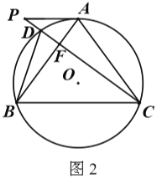
(1)如图1,若![]() 为
为![]() 延长线上一点,连
延长线上一点,连![]() ,求证:
,求证:![]() 平分
平分![]() .
.

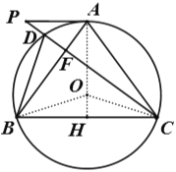
(2)如图2,若![]() 于
于![]() ,过
,过![]() 点作圆的切线
点作圆的切线![]() 交直线
交直线![]() 于
于![]() ,若
,若![]() ,求
,求![]() .
.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)先根据圆内接四边形的性质可得![]() ,从而可得
,从而可得![]() ,再根据等腰三角形的性质可得
,再根据等腰三角形的性质可得![]() ,从而可得
,从而可得![]() ,然后根据圆周角定理可得
,然后根据圆周角定理可得![]() ,从而可得
,从而可得![]() ,最后根据角平分线的定义即可得证;
,最后根据角平分线的定义即可得证;
(2)法1:先根据圆的切线的性质可得![]() ,再根据垂直平分线的判定与性质可得
,再根据垂直平分线的判定与性质可得![]() ,从而可得
,从而可得![]() ,然后根据平行线分线段成比例定理可得
,然后根据平行线分线段成比例定理可得![]() ,最后根据正弦三角函数、勾股定理可求出AF、BF的长,由此即可得;法2:先同法1得出
,最后根据正弦三角函数、勾股定理可求出AF、BF的长,由此即可得;法2:先同法1得出![]() ,再根据等腰三角形的性质、圆周角定理可得
,再根据等腰三角形的性质、圆周角定理可得![]() ,从而可得
,从而可得![]() ,设
,设![]() ,利用正弦三角函数、勾股定理可得
,利用正弦三角函数、勾股定理可得![]() ,然后利用垂径定理可得
,然后利用垂径定理可得![]() ,设
,设![]() ,最后在
,最后在![]() 和
和![]() 中,分别利用勾股定理列出等式可求出x的值,从而可得BF的值,由此即可得.
中,分别利用勾股定理列出等式可求出x的值,从而可得BF的值,由此即可得.
(1)∵四边形![]() 内接于
内接于![]()
∴![]()
又∵![]()
∴![]()
∵![]()
∴![]()
![]()
由圆周角定理得:![]()
∴![]()
∴![]() 平分
平分![]() ;
;
(2)法1:连![]() 并延长交
并延长交![]() 于
于![]() ,连
,连![]() ,
,![]()
![]()
![]() 切圆于
切圆于![]()
![]()
![]()
又![]()
![]() ,
,![]()
![]() AH是线段BC的垂直平分线
AH是线段BC的垂直平分线
![]()
![]()
![]()
![]()
![]()
![]()
由圆周角定理得:![]()
![]()
![]()
![]() 在
在![]() 中,
中,![]()
设![]() ,则
,则![]()
![]()
![]() ,
,![]() ,
,![]()
则![]() ;
;
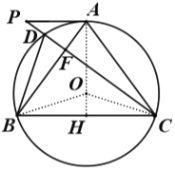
法2:连![]() 并延长交
并延长交![]() 于
于![]() ,连
,连![]() ,
,![]()
![]()
![]() 切圆于
切圆于![]()
![]()
![]()
又![]()
![]() ,
,![]()
![]() AH是线段BC的垂直平分线
AH是线段BC的垂直平分线
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]() (等腰三角形的三线合一)
(等腰三角形的三线合一)
由圆周角定理得:![]()
![]()
![]()
![]()
设![]() ,则
,则![]()
![]() ,
,![]() ,
,![]()
由垂径定理得:![]()
设![]() ,则
,则![]()
由勾股定理得:![]()
即![]()
解得![]()
![]()
![]() ,
,![]()
则![]() .
.


科目:初中数学 来源: 题型:
【题目】学生在素质教育基地进行社会实践活动,帮助农民伯伯采摘了黄瓜和茄子共40kg,了解到这些蔬菜的种植成本共42元,还了解到如下信息:

(1)请问采摘的黄瓜和茄子各多少千克?
(2)这些采摘的黄瓜和茄子可赚多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(-3,0)、点B(0,![]() ),直线
),直线![]() 与x轴、y轴分别交于点D、C,M是平面内一动点,且∠AMB=60°,则MCD面积的最小值是 ________.
与x轴、y轴分别交于点D、C,M是平面内一动点,且∠AMB=60°,则MCD面积的最小值是 ________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
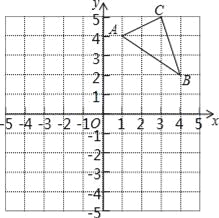
(1)请画出△A1B1C1,使△A1B1C1与△ABC关于x轴对称;
(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出点B旋转到点B2所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强居民节水意识,我市自来水公司采用以户为单位分段计费办法收费,即每月用水不超过10吨,每吨收费![]() 元;若超过10吨,则10吨水按每吨
元;若超过10吨,则10吨水按每吨![]() 元收费,超过10吨的部分按每吨
元收费,超过10吨的部分按每吨![]() 元收费,公司为居民绘制的水费
元收费,公司为居民绘制的水费![]() (元)与当月用水量
(元)与当月用水量![]() (吨)之间的函数图象如下,则下列结论错误的是( )
(吨)之间的函数图象如下,则下列结论错误的是( )
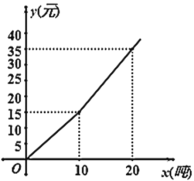
A.![]()
B.![]()
C.若小明家3月份用水14吨,则应缴水费23元
D.若小明家7月份缴水费30元,则该用户当月用水![]() 吨
吨
查看答案和解析>>
科目:初中数学 来源: 题型:
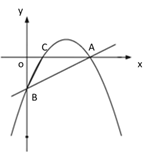
【题目】【题目】如图①,一次函数 y=![]() x - 2 的图像交 x 轴于点 A,交 y 轴于点 B,二次函数 y=
x - 2 的图像交 x 轴于点 A,交 y 轴于点 B,二次函数 y=![]() x2 bx c的图像经过 A、B 两点,与 x 轴交于另一点 C.
x2 bx c的图像经过 A、B 两点,与 x 轴交于另一点 C.
(1)求二次函数的关系式及点 C 的坐标;
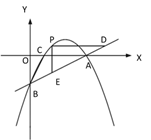
(2)如图②,若点 P 是直线 AB 上方的抛物线上一点,过点 P 作 PD∥x 轴交 AB 于点 D,PE∥y 轴交 AB 于点 E,求 PD+PE 的最大值;
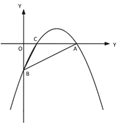
(3)如图③,若点 M 在抛物线的对称轴上,且∠AMB=∠ACB,求出所有满足条件的点 M的坐标.
① ② ③
查看答案和解析>>
科目:初中数学 来源: 题型:
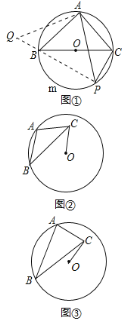
【题目】(1)问题背景:如图①,BC是⊙O的直径,点A在⊙O上,AB=AC,P为![]() 上一动点(不与B,C重合),求证:
上一动点(不与B,C重合),求证:![]() PA=PB+PC.请你根据图中所给的轴助线,给出作法并完成证明过程.
PA=PB+PC.请你根据图中所给的轴助线,给出作法并完成证明过程.
(2)类比迁移:如图②,⊙O的半径为3,点A,B在⊙O上,C为⊙O内一点,AB=AC,AB⊥AC,垂足为A,求OC的最小值
(3)拓展延伸:如图③,⊙O的半径为3,点A,B在⊙O上,C为⊙O内一点,AB=![]() AC,AB⊥AC,垂足为A,则OC的最小值为____________.
AC,AB⊥AC,垂足为A,则OC的最小值为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AC=BC=4,∠ACB=90°,正方形BDEF的边长为2,将正方形BDEF绕点B旋转一周,连接AE、BE、CD.
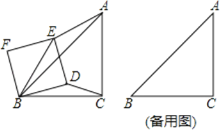
(1)请找出图中与△ABE相似的三角形,并说明理由;
(2)求当点E在线段AF上时CD的长;
(3)设AE的中点为M,连接FM,试求FM长的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com