
【题目】新学期开始时,某校九年级一班的同学为了增添教室绿色文化,打造温馨舒适的学习环境,准备到一家植物种植基地购买A、B两种花苗.据了解,购买A种花苗3盆,B种花苗5盆,则需210元;购买A种花苗4盆,B种花苗10盆,则需380元.
(1)求A、B两种花苗的单价分别是多少元?
(2)经九年级一班班委会商定,决定购买A、B两种花苗共12盆进行搭配装扮教室.种植基地销售人员为了支持本次活动,为该班同学提供以下优惠:购买几盆B种花苗,B种花苗每盆就降价几元,请你为九年级一班的同学预算一下,本次购买至少准备多少钱?最多准备多少钱?
【答案】(1)A、B两种花苗的单价分别是20元和30元;(2)本次购买至少准备240元,最多准备290元
【解析】
(1)设A、B两种花苗的单价分别是x元和y元,则![]() ,即可求解;
,即可求解;
(2)设购买B花苗x盆,则购买A花苗为(12﹣x)盆,设总费用为w元,由题意得:w=20(12﹣x)+(30﹣x)x=﹣x2+10x+240(0≤x≤12),即可求解.
解:(1)设A、B两种花苗的单价分别是x元和y元,则![]() ,解得
,解得![]() ,
,
答:A、B两种花苗的单价分别是20元和30元;
(2)设购买B花苗x盆,则购买A花苗为(12﹣x)盆,设总费用为w元,
由题意得:w=20(12﹣x)+(30﹣x)x=﹣x2+10x+240(0≤x≤12),
∵-1<0.故w有最大值,当x=5时,w的最大值为265,当x=12时,w的最小值为216,
故本次购买至少准备216元,最多准备265元.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AC=BC=4,∠ACB=90°,正方形BDEF的边长为2,将正方形BDEF绕点B旋转一周,连接AE、BE、CD.
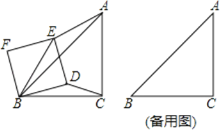
(1)请找出图中与△ABE相似的三角形,并说明理由;
(2)求当点E在线段AF上时CD的长;
(3)设AE的中点为M,连接FM,试求FM长的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为
为![]() 的直径,点
的直径,点![]() 是
是![]() 右侧半圆上的一个动点,点
右侧半圆上的一个动点,点![]() 是
是![]() 左侧半圆的中点,
左侧半圆的中点,![]() 是
是![]() 的切线,切点为
的切线,切点为![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .点
.点![]() 为射线
为射线![]() 上一动点,连接
上一动点,连接![]() ,
,![]()
![]() ,
,![]() .
.
(1)当![]() 时, 求证:
时, 求证:![]() .
.
(2)若![]() 的半径为
的半径为![]() ,请填空:
,请填空:
①当四边形![]() 为正方形时,
为正方形时,![]()
②当![]() 时, 四边形
时, 四边形![]() 为菱形.
为菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=12,AD=15,E是CD上的点,将△ADE沿折痕AE折叠,使点D落在BC边上点F处,点P是线段CB延长线上的动点,连接PA,若△PAF是等腰三角形,则PB的长为____.
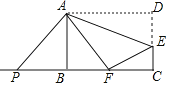
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=﹣1,下列结论不正确的是( )
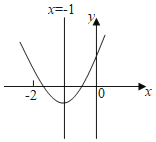
A.b2>4acB.abc>0
C.a﹣c<0D.am2+bm≥a﹣b(m为任意实数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的图象经过A(1,0),B(3,0),C(0,6)三点.
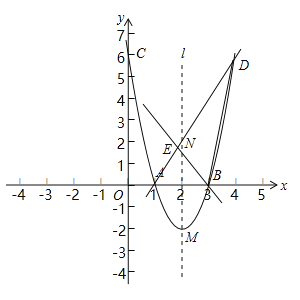
(1)求抛物线的解析式.
(2)抛物线的顶点M与对称轴l上的点N关于x轴对称,直线AN交抛物线于点D,直线BE交AD于点E,若直线BE将△ABD的面积分为1:2两部分,求点E的坐标.
(3)P为抛物线上的一动点,Q为对称轴上动点,抛物线上是否存在一点P,使A、D、P、Q为顶点的四边形为平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
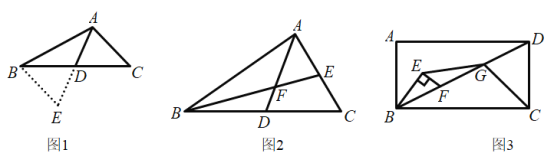
小红遇到这样一个问题:如图1,![]() 中,
中,![]() ,
,![]() ,AD是中线,求AD的取值范围.她的做法是:延长AD到E,使
,AD是中线,求AD的取值范围.她的做法是:延长AD到E,使![]() ,连接BE,证明
,连接BE,证明![]() ,经过推理和计算使问题得到解决.
,经过推理和计算使问题得到解决.
请回答:(1)小红证明![]() 的判定定理是:__________________________________________;
的判定定理是:__________________________________________;
(2)AD的取值范围是________________________;
方法运用:
(3)如图2,AD是![]() 的中线,在AD上取一点F,连结BF并延长交AC于点E,使
的中线,在AD上取一点F,连结BF并延长交AC于点E,使![]() ,求证:
,求证:![]() .
.
(4)如图3,在矩形ABCD中,![]() ,在BD上取一点F,以BF为斜边作
,在BD上取一点F,以BF为斜边作![]() ,且
,且![]() ,点G是DF的中点,连接EG,CG,求证:
,点G是DF的中点,连接EG,CG,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生每天的睡眠情况,某初中学校从全校800名学生中随机抽取了40名学生,调查了他们平均每天的睡眠时间(单位:h),统计结果如下:9,8,10.5,7,9,8,10,9.5,8,9,9.5,7.5,9.5,9,8.5,7.5,10,9.5,8,9,7,9.5,8.5,9,7,9,9,7.5,8.5,8.5,9,8,7.5,9.5,10,9.5,8.5,9,8,9.在对这些数据整理后,绘制了如图的统计图表:
睡眠时间分组统计表:
组别 | 睡眠时间分组 | 人数(频数) |
1 | 7≤t<8 | m |
2 | 8≤t<9 | 11 |
3 | 9≤t<10 | n |
4 | 10≤t<11 | 4 |
请根据以上信息,解答下列问题:
(1)m= ,n= ,a= ,b= ;
(2)抽取的这40名学生平均每天睡眠时间的中位数落在 组(填组别);在扇形统计图中,第4组所在扇形的圆心角是 度;
(3)如果按照学校要求,学生平均每天的睡眠时间应不少于9h.请估计该校学生中睡眠时间符合要求的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
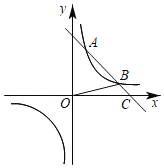
【题目】如图,在平面直角坐标系xOy中,一次函数y=﹣x+b的图象与反比例函数![]() (k>0)的图象相交于A,B两点,与x轴相交于点C(4,0),且点B(3,n),连接OB.
(k>0)的图象相交于A,B两点,与x轴相交于点C(4,0),且点B(3,n),连接OB.
(1)求一次函数和反比例函数的表达式;
(2)求△BOC的面积;
(3)将直线AB向下平移,若平移后的直线与反比例函数的图象只有一个交点,试说明直线AB向下平移了几个单位长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com