
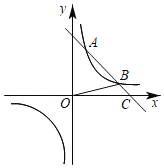
【题目】如图,在平面直角坐标系xOy中,一次函数y=﹣x+b的图象与反比例函数![]() (k>0)的图象相交于A,B两点,与x轴相交于点C(4,0),且点B(3,n),连接OB.
(k>0)的图象相交于A,B两点,与x轴相交于点C(4,0),且点B(3,n),连接OB.
(1)求一次函数和反比例函数的表达式;
(2)求△BOC的面积;
(3)将直线AB向下平移,若平移后的直线与反比例函数的图象只有一个交点,试说明直线AB向下平移了几个单位长度.
【答案】(1)y=﹣x+4,y=![]() ;(2)2;(3)4+2
;(2)2;(3)4+2![]() 或4﹣2
或4﹣2![]()
【解析】
(1)用待定系数法即可求解;
(2)△BOC的面积=![]() OC×BD=
OC×BD=![]() ×4×1=2;
×4×1=2;
(3)直线AB向下平移m个单位后和反比例函数只有一个公共点,则![]() =﹣x+4﹣m,整理得:x2+(m﹣4)x+3=0,△=b2﹣4ac=0,即可求解.
=﹣x+4﹣m,整理得:x2+(m﹣4)x+3=0,△=b2﹣4ac=0,即可求解.
(1)将点C的坐标代入一次函数表达式y=﹣x+b并解得:b=4,
故一次函数的表达式为:y=﹣x+4,
将点B的坐标代入y=﹣x+4得:n=﹣3+4=1,故点B(3,1),
将点B的坐标代入反比例函数表达式并解得:k=3,
故反比例函数表达式为:y=![]() ;
;
(2)过点B作BD⊥x轴于点D,则BD=1,又OC=4,

则△BOC的面积=![]() OC×BD=
OC×BD=![]() ×4×1=2;
×4×1=2;
(3)将直线AB向下平移m个单位(m>0)得到直线的表达式为:y=﹣x+4+m,
∵直线AB向下平移m个单位后和反比例函数只有一个公共点,则![]() =﹣x+4﹣m,整理得:x2+(m﹣4)x+3=0,
=﹣x+4﹣m,整理得:x2+(m﹣4)x+3=0,
∴△=b2﹣4ac=(m﹣4)2﹣4×1×3=0,解得:m=4±2![]() ,
,
故直线AB向下平移了4+2![]() 或4﹣2
或4﹣2![]() 个长度单位.
个长度单位.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】新学期开始时,某校九年级一班的同学为了增添教室绿色文化,打造温馨舒适的学习环境,准备到一家植物种植基地购买A、B两种花苗.据了解,购买A种花苗3盆,B种花苗5盆,则需210元;购买A种花苗4盆,B种花苗10盆,则需380元.
(1)求A、B两种花苗的单价分别是多少元?
(2)经九年级一班班委会商定,决定购买A、B两种花苗共12盆进行搭配装扮教室.种植基地销售人员为了支持本次活动,为该班同学提供以下优惠:购买几盆B种花苗,B种花苗每盆就降价几元,请你为九年级一班的同学预算一下,本次购买至少准备多少钱?最多准备多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近日,在公安部交通管理局部署下,全国各地交警都在大力开展|一盔一带安全守护行动,为了解市民对骑电动车戴头盔的赞同情况,某课题小组随机调查了部分市民,并根据调查结果绘制了尚不完整的统计图.
根据以上统计图回答一下问题:
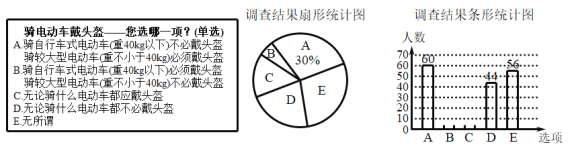
(1)这次调查的市民共_______人;
(2)若选择![]() 的人数是选择
的人数是选择![]() 的人数的3倍,则扇形统计图中,扇形
的人数的3倍,则扇形统计图中,扇形![]() 的圆心角度数是______;
的圆心角度数是______;
(3)补全条形统计图;
(4)若该市约有80万人,请估计安全意识淡薄(选择D或E)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
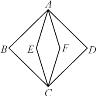
【题目】定义:如图,若菱形AECF与正方形ABCD两个顶点A,C重合,另外两个顶点E,F在正方形ABCD的内部,则称菱形AECF为正方形ABCD的内含菱形.
若正方形的周长为16,其内含菱形边长是整数,则内含菱形的周长为________;
若正方形的面积为18,其内含菱形的面积为6,则内含菱形的边长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.
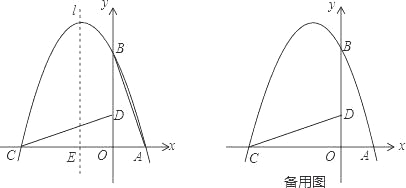
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t,
①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似时,点P的坐标;
②是否存在一点P,使△PCD的面积最大?若存在,求出△PCD的面积的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售![]() ,
,![]() 两种商品,售出2件
两种商品,售出2件![]() 种商品和3件
种商品和3件![]() 种商品所得利润为700元;售出3件
种商品所得利润为700元;售出3件![]() 种商品和5件
种商品和5件![]() 种商品所得利润为1100元.
种商品所得利润为1100元.
(1)求每件![]() 种商品和每件
种商品和每件![]() 种商品售出后所得利润分别为多少元;
种商品售出后所得利润分别为多少元;
(2)由于需求量大,![]() ,
,![]() 两种商品很快售完,商场决定再一次购进
两种商品很快售完,商场决定再一次购进![]() ,
,![]() 两种商品共34件,如果将这34件商品全部售完后所得利润不低于4000元,那么此商场至少需购进多少件
两种商品共34件,如果将这34件商品全部售完后所得利润不低于4000元,那么此商场至少需购进多少件![]() 种商品.
种商品.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意得( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在RtΔABC中,∠C=90°,∠BAC的角平分线AD交BC边于D,以AB上某一点O为圆心作⊙O,使⊙O经过点A和点D,与AB边的另一个交点为E.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为4,∠B=30°.求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
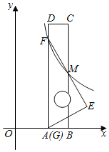
【题目】如图,将一把矩形直尺ABCD和一块含30°角的三角板EFG摆放在平面直角坐标系中,AB在x轴上,点G与点A重合,点F在AD上,三角板的直角边EF交BC于点M,反比例函数![]() (x
(x![]() 0)的图象恰好经过点F,M.若直尺的宽CD=2,三角板的斜边FG=
0)的图象恰好经过点F,M.若直尺的宽CD=2,三角板的斜边FG=![]() ,则k=____.
,则k=____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com